Оглавление:









Асимметрический волчок в физике
- Асимметричный топ. Примените уравнения Эйлера к более сложной задаче свободного вращения асимметричных вершин со всеми тремя различными моментами инерции. Для ясности ч> ч> ч (37,1) Два интеграла уравнений Эйлера известны заранее.
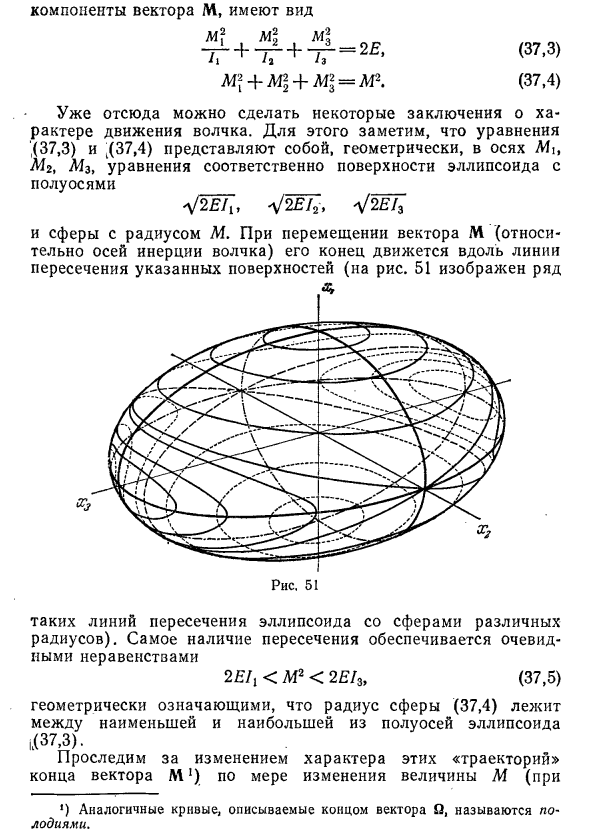
Они задаются законом сохранения энергии и импульса и представлены равенством Iifli + h & 2 + / 3 ^ 3 =, 7 В ilnl + ilnl + ijsil = M \ 1 J Где приведены абсолютные значения энергии E и момента M Постоянная. Эти два уравнения, выраженные через компоненты вектора М, имеют вид Ml + Ml + Ml = 2E, (37,3) J-2 ± 3 Ml + m | + M32 = M2. (37,4) Уже отсюда мы можем сделать некоторые выводы о характере верховного движения.
его концы движутся вдоль пересечения указанных поверхностей Людмила Фирмаль
По этой причине уравнение (37.3) И (37.4) геометрически представлены осями Mi, M2, M3. Уравнение, соответствующее поверхности полуосного эллипсоида y / 2EIi, y / 2E12, y / 2E1z При перемещении вектора M (относительно верхней инерционной оси) (на рисунке 51 показана серия таких пересечений сфер с различными радиусами от эллипса). Показано).
Само пересечение обеспечивается очевидным неравенством 2Eh 2 E12 (В противном случае индексы 1 и 3 должны быть перемещены во всех следующих выражениях): (37,6) И положительный параметр k2 <1 тогда , 2 = (ч-ч) (2EIs-m 2), 7 В (I3-ч) (М * -2 Е ч) ‘{’ -I a / (1-s2d) s (l-k2s2) (Справочное время R ^ 2-0).
- Когда этот интеграл инвертирован, он происходит, как известно Но одна из эллиптических функций Якоби s-sn t Определение временной зависимости P2. Функция Ft2 (t) И fts (t) выражаются алгебраически относительно P2 (Ј) согласно уравнению (37.6).
Рассмотрим определение двух других эллиптических функций cn m = \ / l-sn2 m, dn m = \ / l-k2 sn2 m, Наконец мы получаем следующее выражение: ^ 1- \ ~ T7t —- FT cn 12E13-м 2 ч (ч-ч) l2EI3-М2 ч (ч-ч) «M2-2Eh ч (ч ~ ч) P2 = \ 7 T: \ sn m (37,10) Y Из (ч-ч) дн Т ‘ Функция (37.10) является периодической, Как известно, переменная m равна 4K, где K — сумма Эллиптический интеграл первого рода: 1 7G / 2 K = [, ds [/ du (37.11) J V (l-s 2) (l-f c 2s 2) J V l-f c 2 sin2 «V 7 0 0
Исходное положение относительно верхней оси Людмила Фирмаль
Таким образом, период дается r = (37,12) По истечении этого времени вектор ft Исходное положение относительно верхней оси. (Сама вершина не возвращается к своей предыдущей позиции относительно системы координат без движения — см. Ниже.) Если 1 \ = 12, не говоря уже о выражении (37.10) Мул, полученный в предыдущем разделе о симметрии Небесная вершина.
Фактически для 1 \ -y 12 параметр k2 -y 0, Эллиптическая функция сводится к кругу: sn t -yinT, cn t -y cost, dn g -y 1 И это возвращается к формуле (36.7). Для M2 = 2E1%: fti = -0, = const, т.е. век Тор ft всегда ориентирован вдоль инерциальной оси zh. оси x%. x Равномерное вращение вокруг оси.
Переходите к абсолютному определению Движущаяся система координат X, Y, Z) верхнего движения пространства как функция времени. Для этого введите углы Эйлера gr, φ, 0 между верхними осями x1, x2j, xz и осями X, Y, Z. Выберите фиксированную ось Z вдоль направления постоянного вектора М.
Поскольку полярный угол и азимут направления Z относительно осей x1, x2 и x% равны, 0 и π / 2-π \) (см. Примечание на стр. 146), то вектор M Ось хх, х2, получить Определить временную зависимость углов 0 и n \). Наряду с компонентами вектора ft они являются периодическими функциями периода (37.12).
Угол φ не входит в уравнение (37.13) Нам нужно взглянуть на уравнение (10), представляющее компонент ft Сквозная дифференциация углов Эйлера. Исключить 0 из уравнения Аналогично, если M2 = 2E1 \ (m = 0) M sin0 simp = Mi = iifti, M sin0 стоимость]; = M2 = / 2 ^ 2, M cos 0 = M3 = / 3L3. (37.13) Отсюда (37.14) Используя уравнение (37.10), (3 dt m + / | 2 2 • (^ r.ibj
Таким образом, функция cp (Ј) определяется квадратурным методом, но подынтегральное выражение содержит эллиптические функции сложным образом. С помощью ряда довольно сложных преобразований этот интеграл можно выразить в виде так называемой тета-функции. Только конечный результат отображается без вычисления х). Функция φ (Ј) равна (максимальная Любая константа сложения) как сумма двух членов
(Из .К и Т- (37.11), (37.12)). Функция в правой части (37.18) _ М -cos Qot = a \ y — 1 sin Qot sin cot-a \ y — 1 cos Qot cos cot, M V Ii V I2 Или, наконец: «= XzP2 V V h VI: (J y — 1 + \ hr ‘2-1 I COS [(По + сo) i] + + I (v l-1- v l _1, cos Как хорошо pzu = (V Tg ~ 1 + V t2 ~ 11s i n + + + f (v l -1- V th-sin [(a ° -tu) *] — Это показывает, что движение вектора pz является суперпозицией двух вращений вокруг оси z с частотой (Qo = b si). 2.
Определите верхнее свободное вращение с M 2 = 2E12. Решения. В этом случае это соответствует структуре на рисунке 3. 51 Переместите конец вектора M вдоль кривой, которая проходит через полюс на оси x2. Уравнение (37.7) принимает следующий вид: ds l 2 , / (ч-ч х ч-ч) ^ P2 * = T = ‘v — w, — * = <Ј ■
Здесь введено обозначение Qo = M / 12 = 2E / M. Интегрируйте это уравнение и используйте уравнение (37.6), чтобы получить л (ч-ч) 1 Ii 1 ° (h-Ii) ch t ′ P2 = П0th t, y 1z (1z-h) ch t Чтобы объяснить абсолютное движение вершин, мы вводим углы Эйлера и определяем 0 как угол между осью Z (направление M) и осью инерции. top x2 (не xs как текст). Относится к уравнениям (37.14), (37.16)
Компонент вектора Q с углами Эйлера должен создавать круговую перестановку с индексом 123- »• 312. Присвойте этим выражениям Формула (1), cos0 = thT, (p = Qot + const, tg ip = —- ~ Г \ ‘ A (- * 3-J-2) Из полученного уравнения видно, что вектор Q асимптотичен (при t oo). приближается к оси x2 и одновременно асимптотически приближается Переместиться на фиксированную ось Z.
Смотрите также:
| Эйлеровы углы в физике | Соприкосновение твердых тел в физике |
| Уравнения Эйлера в физике | Движение в неинерциальной системе отсчета |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

