



Правило отрезков и правило центра тяжести весового треугольника в тройных системах
В тройном изотермическом разрезе можно определить состав и соотношение равновесных фаз в двухфазной и трехфазной областях.
- Правило сегмента (плечо) используется в двухфазной области, а правило центра тяжести весового треугольника используется в области трехфазного равновесия. Рисунок 4.4 представляет собой изотермический разрез диаграммы равновесия с неограниченной растворимостью компонентов в жидком и твердом состоянии.
В двухфазной области конод, соединяющий точки состава равновесной фазы твердого раствора и жидкости на твердой и жидкой изотермах соответственно, строится либо экспериментально, либо расчетным путем.
Исходя из геометрической термодинамики, конод двухфазной области con + の в изотермическом сечении представляет собой изоактивную линию, то есть соединяет точки с одинаковым значением термодинамической активности каждого компонента в соседней однофазной области.
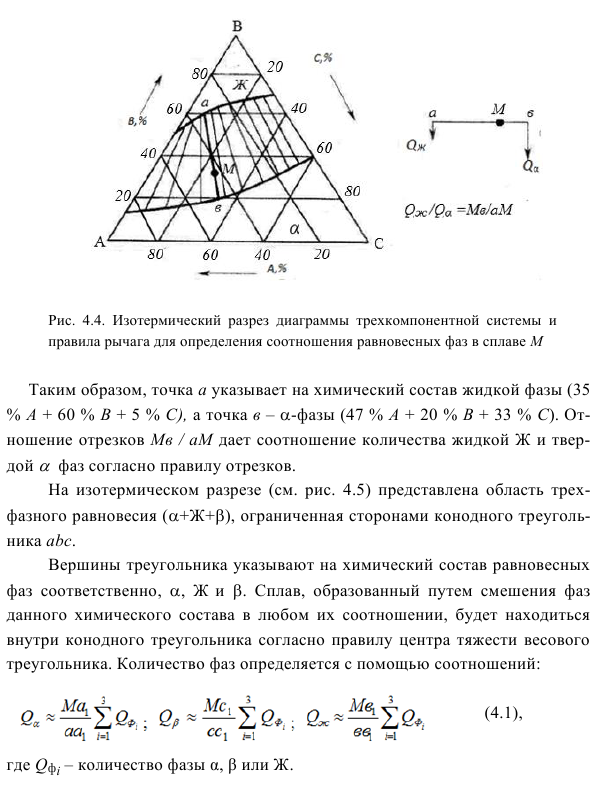
Это становится. 36 Рисунок 4.4. Правило рычага для определения соотношения фазы равновесия диаграммы тройной системы и фазы равновесия сплава М.
Таким образом, точка А представляет собой химический состав жидкой фазы (35% А + 60% В + 5% С)
Показано, что точка B является министром (47% A + 20% B + 33% C) Отношение сегментов Mv / aM указывает отношение жидкой фазы к объему твердой фазы в соответствии с правилами сегмента. Изотермический разрез (см. Рис. 4.5) показывает трехфазную область равновесия ( + Ж + ), окруженную сторонами треугольника конодо abc.
Вершины треугольника указывают химический состав фаз равновесия фаз,, и соответственно. Сплав, образованный смешиванием фаз данного химического состава в любом соотношении, будет находиться внутри конического треугольника в соответствии с правилом центра тяжести гравитационного треугольника.
Количество фаз определяется с помощью соотношения (4.1). Где Qphi — число фаз α, β или G. 37 Рисунок 4.5. Используя это правило и центр тяжести весового треугольника путем определения изотермического сечения диаграммы ABC системы и равновесного фазового отношения сплава М, можно решить два типа проблем:
- а) с использованием известного состава сплава И найти химический состав равновесной фазы и ее соотношение;
- б) определить положение целевого сплава (его химический состав) из соотношения фаз. Вот пример использования этих правил в изотермической части диаграммы равновесия A — B — C.
Определите соотношение равновесной фазы, и сплава (точка М), состав которого составляет 20% А, 40% В, а остальное — С. C. Вспомогательная линия проведена на пересечении вершины треугольника конода и точки М. Есть отверстия AB, AC, BC (см. Рисунок 4.5, а).
Получить точки пересечения a1, b1 и c1. Затем используйте уравнение (4.1), чтобы определить количество фаз. П р и м е р 2. Если соотношение фаз Qα: Qβ: Qж = 1: 2: 3:, найти химический состав сплава (положение точки Х) и состав равновесной фазы. 38 Сначала определите химический состав равновесной фазы.
Это определяется положением вершин треугольников конодитов a, b и c и соответствует следующему: Жидкая фаза — 45% A, 20% B, остаточный -C, фаза-фаза — 16% A, 25% B и другие -C, жидкая фаза — 15% A, 65% B, остальное — C (рис. 4.5).
Далее используйте правило сегмента, чтобы разделить стороны треугольника ab конода в соотношении 1: 3 и соединить вершины в вычисленной точке c1 (рис. 4.5, б). Затем разделите ребро bc на соотношение 2: 3 и соедините вершину a с положением вычисленной точки a1.
- Пересечение линий cc1 и aa1 является желаемой точкой состава сплава. Сегмент bb1 проходит через ту же точку и делит сторону ac на соотношение 1: 2, как в проблемном состоянии. Следовательно, требуемый состав сплава соответствует 20% А, 40% В и 40% С.
Смотрите также:
Примеры решения задач по материаловедению

