Оглавление:









Тензор инерции в физике
- Тензор инерции. Чтобы рассчитать кинетическую энергию твердого тела, рассмотрим ее как дискретную систему материальных точек. Здесь все делается для всех точек, составляющих тело. Здесь и далее индекс, который нумерует эти точки, опущен, чтобы упростить запись выражения. Подставляя здесь (31.2), m = Ј J (V + [Sir]) 2 = Ј = V2 + ЈmV [Slг] + Ј2 [Prf. Скорость V и ft одинаковы во всех точках тела. по Это первый период V2 / 2 выполняется по итоговому знаку и сумме 5 ^ га — масса тела, обозначенная буквой q.
Второй термин записывается следующим образом: 5 ^ raV [ftr] = 5 ^ rar [Vft] = [Vft] 5 ^ rar. Это указывает на то, что если начало координат движущейся системы координат выбрано в соответствии с согласованием в центре инерции, этот член исчезнет, поскольку в этом случае e = 0.
кинетическая энергия твердого тела Выражается как сумма двух частей Людмила Фирмаль
Наконец, откройте квадрат векторного произведения в третьем члене В результате мы находим m = ^ + \ Y, m # 2r2- (32L) Следовательно, . Первый член (32.1) — кинетическая энергия трансляции. Похоже, что вся масса тела сосредоточена в центре инерции. Второе слагаемое — это кинетическая энергия вращательного движения с угловой скоростью Q.
Ось, которая проходит через центр инерции. Подчеркивается, что возможность такого разделения кинетической энергии на две части зависит от выбора начала координат системы координат, точно связанной с центром инерции тела.
- Переписать кинетическую энергию вращения тензора Обозначение, т. Е. Вектор r, составляющая C1 1): Твр = у ^ ^ ^ икси ^ к ^ к} = -2 ^ ^ = ^ ^ TYljxi X ^ X ^). Где мы использовали тождество, где & ik-тождество Тензор (если i = k и ноль, компонент равен 1 когда я ф к). Введение тензора hk = Yim (xfbik-XiXk), (32,2) Получить окончательную формулу для кинетической энергии твердого тела в форме m = ^ + \ h k ^ k- (32,3) Лагранжева функция твердого тела взята из (32.3)
Чтение потенциальной энергии L = ^ + \ h k ^ k- а. (32,4) Потенциальная энергия, как правило, является функцией шести переменных, которые определяют положение твердого тела. Например, три координаты X, Y и Z центра инерции и три угла, которые определяют направление оси подвижной координаты относительно фиксированной координаты.
Для ясности опишите компонент в явном виде Следующая таблица Людмила Фирмаль
Tensor Ck — момент тензора инерции или Просто тензор инерции тела. Как ясно из определения (32.2), Симметричный, то есть Iik = привет- (32,5) : (От Ylm (y2 + z <1) до T, чт -‘Y] thr \ Iik = -T, tx X) t (x2 + z1) -Y jnyz. (32,6) \ -Y jn zx — jnzyЈ) t (x2 + y2)) Компоненты / LJ, Iyy, Izz иногда называют моментами инерции относительно соответствующих осей.
Тензор инерции явно аддитивен — момент инерции Тело равно сумме его моментов инерции. Если твердое тело можно считать твердым, По определению (32.2) сумма заменяется на интеграл от объема тела. Iik = j p ip ^ l & ik% i% k) dV. (32,7) Подобно симметричному тензору второго ранга, Инерция может быть уменьшена по диагонали путем правильного выбора направления осей x1, x2, x%.
Эти направления называются главными осями инерции, а соответствующие значения тензорных компонент называются главными моментами инерции и обозначаются как ii, / 2 и / 3. Выбрав эту ось Вращательная кинетическая энергия # 1, # 2, xs особенно легко выражается. твр = \ (м 2 + м \ + мл) — (32,8)
Каждый из трех основных моментов инерции Может быть больше, чем сумма двух других. так h + h = X) w (x \ + x \ + 2a? h) ^ X) m (x \ + x ) = 73. (32,9) Объекты, у которых все три основных момента инерции различаются Они называются асимметричными вершинами. Если два основных момента инерции равны друг другу, 1 \ = Если = / 2Ф / 3, то тело называется симметричным волчком.
В этом случае выбор направления главной оси плоскости X \ X2 Любой. Если все три основных момента инерции совпадают, Ло называется мяч сверху. В этом случае выбор всех трех инерционных шпинделей является произвольным. Можно рассмотреть три оси, которые ортогональны друг другу.
Найти главную ось инерции очень легко Твердое тело имеет ту или иную симметрию. Очевидно, что положение центра инерции и направление главной оси должны иметь одинаковую симметрию. Так что, если тело имеет плоскость симметрии, Инерция должна быть в этой плоскости.
Есть два из них Основная ось инерции, а третья перпендикулярна ей. Очевидный случай такого рода — система частиц в одной плоскости. В этом случае существует простая взаимосвязь между тремя основными моментами инерции. если Плоскость системы выбрана в качестве плоскости х \ х2.
Это для всех частиц х% = 0 Ii = Y, mxl, I2 = 52mxl, / 3 = 52m (xl + x%), Вот так Из = h + I2. (32.10) Если тело имеет ось симметрии любого порядка, Центр инерции находится на этой оси. Это соответствует одному Из инерциальных осей две другие перпендикулярны ему. Кроме того, если порядок оси симметрии выше, чем у второй оси, тело симметрично сверху.
Фактически, каждая большая ось (перпендикулярная оси симметрии) может поворачиваться на угол, отличный от 180 °. Выберите эти оси Неоднозначно, это возможно только с симметричным верхом. Особый случай — система частиц По прямой.
Если вы выберите эту строку как Ось х3, то все частицы х \ = х2 = 0, поэтому две основные Моменты инерции постоянны, а третий равен нулю. / 1 = / 2 = 4t 4 / s = 0. (32.11) Такая система называется ротором. В отличие от общего случая любого корпуса, характерная функция ротора Он имеет только две вращательные степени свободы (не три), соответствующие вращению вокруг осей x \ и x2 .
Очевидно, что нет смысла говорить о вращении линии вокруг себя. Напоследок скажу еще одну вещь о расчете Тензор инерции. (Этот тензор был определен относительно системы координат, начало которой находится в центре инерции, но основная формула (32.3) справедлива только с этим определением) Однако может оказаться полезным заранее рассчитать аналогичный тензор для его расчета.
4 = Јm (x ‘2ib ik-x [x’k), Определено относительно другого начала O ‘. Если расстояние O O1 задано вектором a, r = r ‘+ a, X {= x [+ a ^ Jik = Jik + And- (o2bik-schak) • (32.12) С помощью этой формулы, зная 1-k, вы можете легко вычислить нужный тензор Задание 1.
Определить основные моменты инерции молекул, которые считаются системами частиц, расположенных на определенном расстоянии друг от друга в следующих случаях: а) Молекула атомов на прямой. Ответ: Ii = h = -Y2 tat12a, h = 0, -V V-Xi Я Где ma — масса атома, а 1ab — расстояние между атомами a и b.
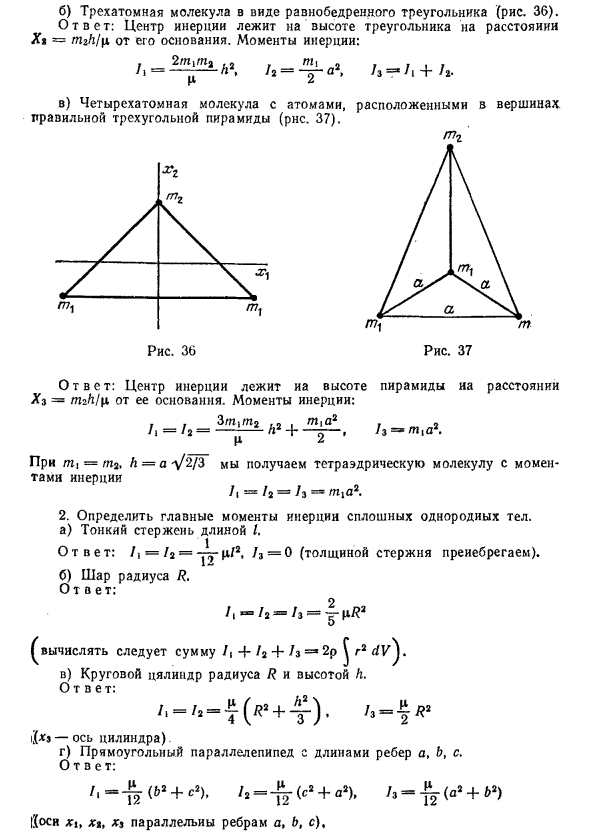
Сумма выполняется для всех пар атомов в молекуле (каждая пара значений a и b включается один раз в сумму). Для двухатомных молекул сумма Один термин, который дает ясные результаты заранее — продукт уменьшения массы обоих атомов и квадрата расстояния между атомами: t \ rp2 г ТП + 777-2 б) Трехатомная молекула в форме равнобедренного треугольника (рис. 36).
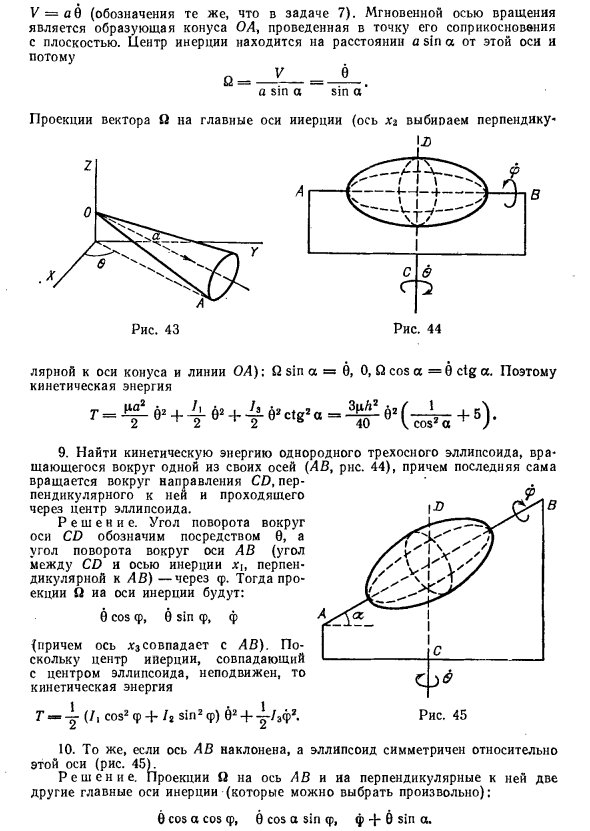
Ответ: Центр инерции находится на высоте лотка. Горник на расстоянии X 2 = rri2h / μ от основания. Момент инерции: 2м1м2, 2 h = ——- h, 1z = Ii + h в) четырехатомная молекула с атомом на вершине равносторонней треугольной пирамиды (рис. 37).
Ответ: Центр инерции находится на высоте пирамиды. Расстояние от основания X $ = rri2h / μ момент инерции 2 3м1м2, 2 ТГц » h = I2 = ———- h N ——— и h = m \ a. ini = 777-2 5 ч = а / 2/3, существует тетраэдрическая молекула с моментом инерции ч = ч = ч 2. Определить главный момент инерции непрерывного однородного тела. а) тонкий стержень I Ответ: 1 \ = / 2 = yd2 / 12, 3 = 0 (без учета толщины стержня).
б) мяч с радиусом i2. Ответ: h = h = h = | cL2 5 (Сумма должна быть рассчитана с 1 \ + / 2 + = 2рф g2 dV). в) цилиндр с радиусом R и высотой h. Ответ: Ii = I2 = ^ (r 2 + ^], h = xD2 (Xs — ось цилиндра). г) прямоугольный параллелепипед с длинами ребер а, 6 и в. Ответ: A = S (62 + c2), m 2- ^ C (s / 2+ .a), 2h / 7-s -M «/ 2 +, j b 2 ) (Оси X2, x3 параллельны ребрам a, 6 и c). г)
Коническая с высотой h и радиусом основания R Решения. Во-первых, тензор 1 [k По отношению к оси, начиная с вершины конуса (рис. 38). Расчет легко сделать в цилиндрических координатах, t / t- / _ 3 f R 2 ч-ч- ^ я ^ + ч Центр тяжести находится на оси конуса на некотором расстоянии, как показывает простой расчет A = 3 / i / 4 сверху.
Наконец, согласно уравнению (32.12) o / b2> 2 «5 я A = h = iI№ = I20 3 Y CD2. е) трехосный эллипсоид с полуосями а, б и в. Решения. Центр инерции совпадает с центром эллипсоида, а главная ось инерции совпадает с этой осью.
Эллиптический объемный интеграл может быть уменьшен до сферического объемного интеграла путем преобразования Координата x = aE „y = br \, z-преобразование уравнения поверхности эллипса сС„ т? + 62 К уравнению поверхности единичной сферы Ј, 2 + Л2 + С2 = 1.
Следовательно, на момент инерции относительно оси х, h = p J J J (y 2 + z2) dxdydz = = pabcJ j J (b 2r \ 2 + c2 C2) dE ^ dx] dC, = ^ I ‘(b2 + c2), Где V — момент инерции единичного радиуса шарика. Учитывая, что объем эллипсоида равен Alabs / 3, мы наконец получаем момент инерции. Т с / 2, 2 часа, т С / 2, 2 часа, г С / 2, 2 часа 1 \ — (b + c), / 2— (a + c), / 3— (a + 6). 3.
Определите частоту небольших колебаний физического маятника (твердое тело, которое колеблется в гравитационном поле вблизи неподвижной горизонтальной оси). Решения. Пусть I — расстояние от центра инерции маятника до оси вращения, а os, | 3, y — углы между направлением оси инерции и осью вращения.
Введите угол в качестве координатной переменной (P между вертикальным и вертикальным падением от центра инерции к оси вращения. Скорость центра инерции равна V = Zf, а проекция — это угол Скорость на главной оси инерции: (pcosa, (pcos | 3, (pcosy. Angle (p Малый, мы находим потенциальную энергию в форме u = \ igl (1-cos cp) <^ Hg / cp2.
Следовательно, функция Лагранжа ] AI2 -2, 1 / г 2, t 2 0, t 2 \ • 2 2 L- ^ Ф2 (^ 1 ^ ”YJФ -— 2— ^ * Следовательно, для частоты колебаний, 2 _ Vgl Il! 2 + h cos2 os + I2 cos2 (3 + / 3 cos2 y * 4. Найти кинетическую энергию системы, показанной на рисунке. Около 39; А AB — это тонкие, однородные стержни длины, которые я поворачиваю в точке A. Штрих O A вращается вокруг точки O (в плоскости фигуры).
Конец B стержня A B скользит вдоль оси Ox. Решения. Скорость центра инерции стержня ОА (расположенного в центре) Является ли Z f / 2. Где (p — угол AO B. Следовательно, кинетическая энергия стержня равна O A. rTr i— V * —2Ф + I 1-; „Ф2 (С — масса одного стержня).
Декартовы координаты центра инерции 39 X стержня AB: (31/2) cos (p Y = (1/2) sin (p. Поскольку угловая скорость вращения этого стержня также равна φ, его кинетическая энергия r2 = ^ (X2 + T2) + -Tf2 = V ^ (1 + 8 sin2φ) φ2 + -1 ^ ~. Общая кинетическая энергия системы T = ^ — (1 + 3sin2φ) φ2 (I = yd2 / 12 заменяется в соответствии с задачей 2). 5. Найти кинетическую энергию цилиндра (радиус R), вращающегося вдоль плоскости.
Масса цилиндра распределяется по всему объему так, что одна из главных осей инерции параллельна оси цилиндра и проходит на определенное расстояние от цилиндра. Момент инерции вокруг этого шпинделя равен I. Решения.
Введите угол (p между вертикальным и вертикальным падением от центра масс к оси цилиндра) (Рисунок 40). Движение цилиндра в каждый момент можно рассматривать как чистое вращение вокруг оси момента, когда линия касается Феномен фиксированной плоскости, угловая скорость этого вращения равна φ (угловая скорость вращения вокруг всех параллельных осей одинакова).
Центр инерции находится на расстоянии l / a2 + R2-2aR cos (p от мгновенной оси и пота 04 .si Rmu Скорость V = fl / a2 + R2-2aRcos (стр. Общая кинетическая энергия А (a2 + R2 2aRcosφ) φ2 + ^ Ф2 * 6. Найти кинетическую энергию однородного цилиндра радиуса а. Рулон внутри цилиндрической поверхности с радиусом R (Рисунок 41). Решения. Вводит угол (p между линией, соединяющей центры обоих цилиндров, и вертикальной линией. Центр инерции вращающегося цилиндра находится на оси, а его скорость V =
Смотрите также:
| Движение в быстро осциллирующем поле | Момент импульса твердого тела |
| Угловая скорость в физике | Уравнения движения твердого тела |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

