Оглавление:




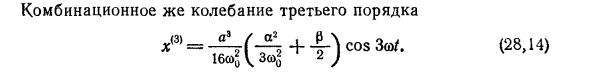

Ангармонические колебания
- Ангармоническая вибрация. Вся теория малых вибраций выше Расширение потенциала системы и кинетической энергии по координатам и скорости. Оставьте только второстепенные условия. Поскольку уравнение движения является линейным, это приближение представляет линейные колебания.
Такое разложение вполне допустимо, если амплитуда колебаний достаточно мала, но, учитывая следующее приближение (так называемая ангармоничность или нелинейность колебаний), это слабая, но качественно новая особенность движения. Он появится.
Для потенциальной энергии член третьего порядка отображается в координате кинетической энергии Людмила Фирмаль
Разверните функцию Лагранжа в Этого заказа. — член, содержащий произведение скорости на координату в форме XiXkXf, это отличие от предыдущего уравнения (23.3) является расширением функции dik (q). связан с выходом из первого порядка член w.
Таким образом, форма функции Лагранжа L = — ^^ (jYijkXjXk hikXiXfo) + r k + \ nrctxkX1- ^ ^ 2 liklXiXkXi, (28,1) g, k, l i, k, l Где Щ и Цы — новые постоянные коэффициенты. Из любой координаты X {если нормально Координата (линейное приближение) Qa, благодаря линейности этого преобразования, третья и четвертая сумма (28.1) заменяется на { Скорость XI Qa и Qa.
- Если сумма этих факторов представлена A, функция Лагранжа получается в следующем виде: l = \ ^ 2 (Qa, — ^ icQic) + + 2 года ‘hotfiyQotQfiQy ~ 2 года] YLoc & yQotQftQy- (28,2) a, | 3, y cx, (3, y Я не пишу уравнение движения, полученное из этой лагранжевой функции полностью.
Важно, чтобы они имели форму Qoc + сviQoc = / cx (Q, Q, Q), (28,3) foe — квадратичная однородная функция с координатой Q Производная во времени. Используя метод последовательного приближения, Решение этих уравнений в виде Q «= Q $ + Q $, (28,4) Где Q a-O? Это нормальная гармоническая вибрация Qa = «0Сcos (шаЈ + аа). (28,5) В следующем приближении справа от уравнения (28.3) оставьте только малый член второго порядка и получите уравнение для величины Qa. malx 4 (2 г)
Поиск решения в серии последовательных форм Приблизительная стоимость Людмила Фирмаль
Соответствующее уравнение движения x + WqX = -ax2- [3×3. (28,9) х = х + х (2) + х ^ с \ далее х = коскат (28.10) Используя точное значение ci, мы ищем себя в виде cu = cuo + cu ^ 1) + a / 2) + … (начальная стадия x ^ Всегда отключается при правильном выборе источника).
Однако в этом случае уравнение движения вида (28,9) Замена его (28.10) не очень удобна, поскольку левая часть уравнения точно не исчезает. Так переписать Предварительный эквивалент X + 1x = -a x 2-0g3- (1-X. (28.11) Поместите x = x ^ + x ^ 2 \ si = sio + si ^ 1) и пропустите термин Если меньше второго порядка, уравнение для х ^ x (2) + cvqx ^ = —osa2 cos2 cot + 2cuocu ^ a cos cut = —cos (2 cut) + 2 cuocu ^ cos cut.
Условие без резонансного члена в правой части уравнения просто дает si ^ = 0 в соответствии с методом нахождения второго приближения, описанным в начале раздела.
Тогда, решив гетерогенное линейное уравнение обычным способом, получим 2 2 x (2) = _m osh_ cog ^ 28L2 ^ 2 (J0q 6 (J0q v 7 v 7 Кроме того, (28.11) x = x ^ + x ^ + x ^ \ si = o) o + a) (2 \ Получить уравнение x ^ + o) qX ^ = —2 axx ^ x ^ — [3 ^ ^ 3 + 2cuocu (2M 1) Или, после простого преобразования, присвойте его правой части выражений (28.10) и (28.12). x (3) + a> aw (3) = -a 3Ј4 + 6ОсСо§cos (Зсvt) + + 2 cuqcu ^ 2 ^ + ba2oc2-> a 2 [a3 cos cut. 6w§4 ^
Уравнивание коэффициента резонансного коэффициента, поскольку обрезание до нуля будет корректировать для основной частоты. Квадратная амплитуда колебаний: ) (2) = (_ _ _ Qp1 8си 12су Рамановская вибрация 3-го порядка cuv (28,13) z <3> = 16cUn (28.14)
Смотрите также:
| Вынужденные колебания при наличии трения | Резонанс в нелинейных колебаниях |
| Параметрический резонанс | Движение в быстро осциллирующем поле |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

