Оглавление:





Потенциальная энергия при растяжении и сжатии
- Потенциальная энергия при растяжении и сжатии Внешние силы, действующие на тело, воздействуют на вызванные ими движения, и энергия деформации — потенциальная энергия накапливается в теле. Из-за накопленной энергии первоначальные размеры тела восстанавливаются при снятии нагрузки. Рассмотрим призму
стержня, растянутую силой P на величину AZ. В процессе нагружения балки сила медленно увеличивается от 0 до P, создавая работу L, численно равную потенциальной энергии деформации при упругой деформации: A = U. В процессе изменения силы вытягивания от 0 до P, тогда (рис. 38, а) дает силу P с несколькими значениями P,
равными AZb удлинения балки {приращение d P i тогда Удлинение является Людмила Фирмаль
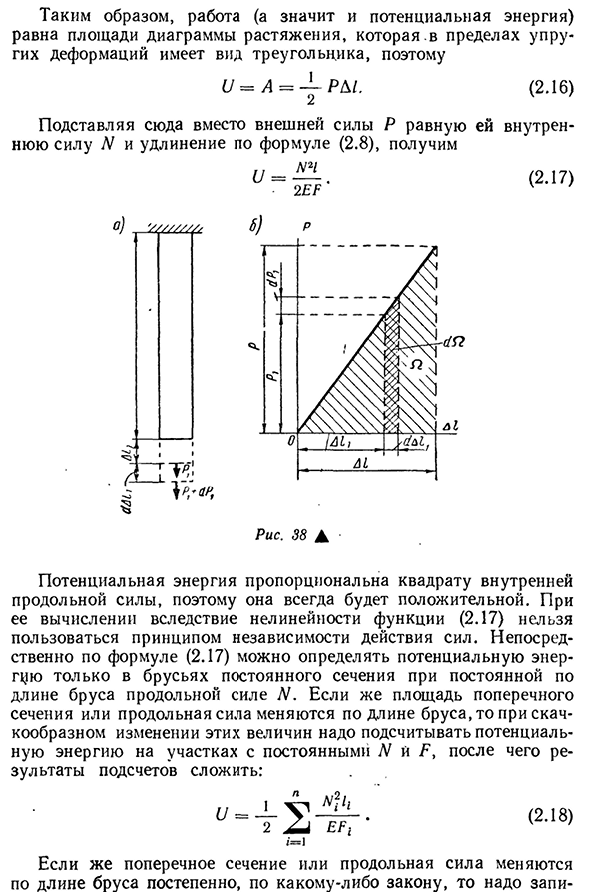
основой силы, увеличенной на величину т / AZp dA = P jdAl i « Для риса. 38, б показана схема растяжения стержня, нагруженного при упругой деформации. На рисунке видно, что значение P1dAZ1 равно площади узкой заштрихованной полосы на диаграмме. дА-DQ, A = J dQ = Q. 41 задание (и, следовательно, потенциальная энергия) равно площади карты растяжения. Поскольку упругая деформация имеет треугольную форму, U = A = -RD1. (2.16) Подставляя здесь, вместо
внешней силы p, найдите внутреннюю силу n, равную ей, и относительное удлинение согласно уравнению (2.8) (2,17) N4 2. ‘ U = Рис 38А а), 2Z /////// Z Поскольку потенциальная энергия пропорциональна квадрату внутренней продольной силы, она всегда положительна. При расчете по функции нелинейности (2.17) невозможно использовать принцип независимости действия силы. Прямым уравнением (2.17) можно определить потенциальную энергию только для стержня постоянного сечения с постоянной
- продольной силой n на длине стержня. Если площадь поперечного сечения или продольная сила изменяется под воздействием луча, потенциальная энергия области с постоянными N и F при этих значениях резко изменяется: (2,18) Согласно некоторым законам, если поперечное или продольное усилие постепенно изменяется вдоль длины стержня, это должно быть записано: 42 — потенциальная энергия бесконечно малого сегмента стержня длиной dx, в течение которого поперечное сечение и внутренняя сила могут считаться
постоянными: N2dx dU = x, 2 £ FX Далее, интегрируйте это выражение по длине полосы: 1p N2dx (/ =. (2.19) 2J EFx ноль Рассмотрим пример определения потенциальной энергии. а) ‘^ 2’4X442. C A = 1 мкг Рис 39А Участок N P R I m e R1. Определить потенциальную энергию медного шагового луча. 39, а, с двумя концентрационными способностями -2 тонны и P2 = 5 т. Модуль упругости материала балки E = 10E кг! На рисунке показана диаграмма продольной силы. 39,6 Примените формулу (2.18) к графику, и вы увидите N2l2N2l3 2EFt + 2 £ F2 + 2EF2 + 20092-30 2-10G-5 20002-20 2-IO6-10 (-3000) М0 2-10G-10 = 34K.G-CM. P p и me p2. Рассчитать потенциальную энергию пучка и его поперечное сечение по линейному закону (рис. 40).
Из-за действия одной концентрирующей силы P продольная направленная сила внутри рассматриваемого пучка является внешней силой. И N = П. Сечение Людмила Фирмаль
на расстоянии х от правого конца 43 балки L / + (^ 2-L) l- один Примените формулу (2.19), и вы увидите Рис 40А Некоторые проблемы используют определенные концепции потенциальной энергии. Это относится к энергии, назначенной единицам начального объема пучка. Это не зависит от размера луча: = JJ_ = 2 _ U ~ Vo ~ Fo / O С тех пор но D / Это один Я — А Е.2 (2.20) Представление относительной деформации из-за напряжения по закону Гука Broadcast
Смотрите также:
| Диаграмма растяжения | Полная работа, затраченная на разрыв образца |
| Сравнение диаграмм растяжения для различных материалов | Истинная диаграмма растяжения |

