Оглавление:




Влияние способа приложения внешней нагрузки и формы стержней на напряжения и деформации
- Влияние метода применения. Форма стержня и напряжение нагрузки Деформация и Уравнения (2.3) и (2.8) получены в предположении, что стержень растягивается равномерной нагрузкой, приложенной к концам. Распределения напряжений и деформаций исследовались
другими методами с применением внешней силы. Возьмите резиновый стержень квадратного сечения и поместите сетку линий, перпендикулярных друг другу, на его поверхности. Рассмотрим деформацию этого стержня под натяжением из-за силы р различными способами приложить эти силы: 1) в виде «Qq-F»
(Рис. 23, а); 2) в форме концентрации р, приложенной к цент- 26,23 ноября Людмила Фирмаль
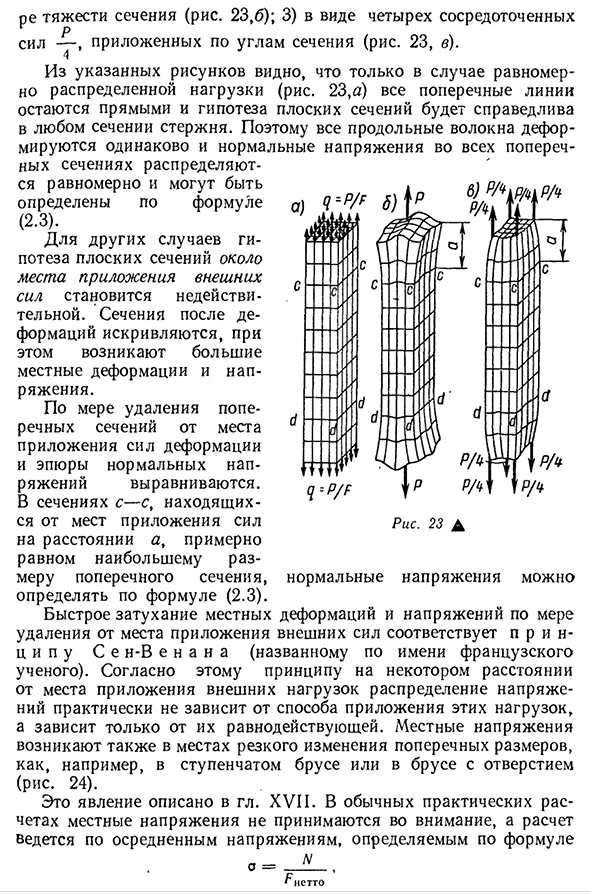
Один * / / / / д / Гравитационное распределение этого сечения (рис. 23,6); 3) Сконцентрировано в четырех формах R R Применяется в углу силового сечения (рис. 23, окт. четыре Из этих рисунков это видно только в случае равномерно распределенной нагрузки (рис. 23 февраля. Поэтому все продольные волокна деформируются одинаково, и нормальное напряжение во всех поперечных сечениях является равномерным. Распределены и могут быть определены по
уравнению (2.3). В других случаях гипотеза о плоском сечении вблизи места приложения внешней силы становится недействительной. Сечение после деформации изгибается, поэтому возникает большая локальная деформация и давление. Поскольку площадь поперечного сечения удаляется от места, где прикладывается сила деформации, график нормального напряжения выравнивается. Сечение C-C
- расположено от места, где сила a прикладывается на расстоянии, приблизительно равном максимальному размеру поперечного сечения, и определяется по уравнению (2.3) Быстрое затухание локальных деформаций и напряжений вдали от места приложения внешних сил происходит в зависимости от французских ученых, согласно этому принципу, на некотором расстоянии от места приложения внешних нагрузок. Фактически, распределение напряжений не зависит от того, как эти нагрузки применяются, а только от результатов. Местные напряжения — это резкие изменения
в поперечных размерах, такие как ступенчатые балки или балки с отверстиями. (Рис. 24). В обычных практических расчетах локальные напряжения не учитываются, и расчет выполняется со средним напряжением, определяемым по формуле Нормальное напряжение нетто 27gde fhett0 — площадь поперечного сечения, работающая на рост л до нетто л общий вес л) — Например, поперечное сечение балки аа показано на рисунке. Где o — размер луча в направлении, перпендикулярном плоскости чертежа. ———— Я ————— ‘ J к — Для ступенчатых стержней и стержней, нагруженных с некоторым усилием, расширение учитывается в постоянных участках H и E, и результаты суммируются алгебраически: д / = 2 ! = 1
Нью-Джерси EFT (2.9) Если эти значения варьируются в соответствии с любым законом непрерывности, D / рассчитывается по формуле Nx DX EFX (2.10)) Где Людмила Фирмаль
NX и FX — нормальные представления силы и площади любого сечения. Давайте рассмотрим пример определения преобразования. 1. Определите изменение длины стального шага. 25, а; Е ~ 2,1 • 106 кг см2 /, f I ~ = 10 см2 \ F2-20 см2. Из состояния равновесия нижней отрезанной секции, секции / — /, // — // и /// — /: NI = PI == 200 кг; N2 = RI-R2 = 200-500 = -300 кг; N-3 = PI — P2 + P3 = 200-500 + 700 = найти внутреннюю силу 400 кг. (На рисунке. 25 ноября. Определим общий рост как сумму роста отдельных участков; PV N2 ^ 3 -Her [EFI 1_LGC EF2 200-50 300-80 _ 300-40 2-106-Ю 2-106-10-2106-20. 400-60 2,106-20 = -4’4 см 28Более 2. Определить удлинение стержня и его площадь поперечного сечения по закону прямой линии (рис. 26 февраля) Нагружен продольными нагрузками, распределенными по линейным законам (рис. 26
февраля) RH = Рис 26А Нормальная сила любого сечения определяется по уравнению Broadcast График нормальной силы показан на рисунке. 26 октября Не расширяет бесконечно малый элемент длины бара DX Индикатор ADX = Nxdx_p0x2__poxdx2LEFOX Полное расширение бара A / = f кд х = F = JJ9 или позже Broadcast O p c2EF0 Ro? В некоторых случаях необходимо определить движение поперечного сечения стержня. 29 февраля Так, например, для бара, показанного на рисунке. 27 августа B-b- и C (рис. 27, б) необходимо определить расширение заштрихованной области между указанными участками.
Смотрите также:
| Продольные силы и их эпюры | Напряжения в сечениях, наклонных к оси стержня при растяжении или сжатии |
| Напряжения и деформации при растяжении и сжатии | Диаграмма растяжения |

