Оглавление:

Виды нагрузок и схематизация элементов сооружений
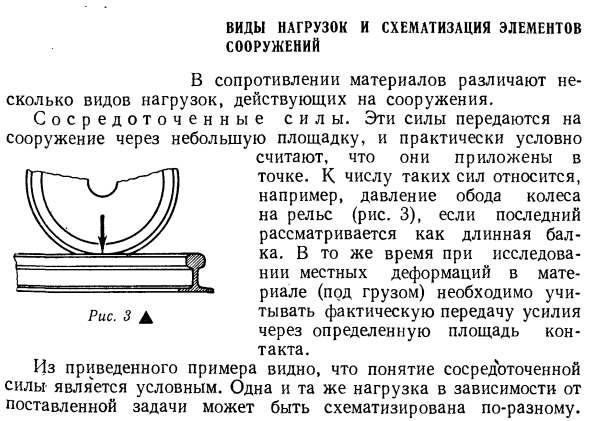
- Тип загрузки и размещение элементов структура Сопротивление материала различает несколько типов нагрузок, действующих на конструкции. Сравнение возможно. Мы считаем, что эти силы передаются на конструкцию через небольшие участки и в какой-то момент применяются почти условно. Такие силы включают, например, давление обода колеса на рельс (рис. 3) (если последний
считается длинным лучом). В то же время при изучении локальной деформации материала (под нагрузкой) необходимо учитывать передачу фактических сил через определенные области контакта. Из приведенного выше примера видно, что понятие концентрации является условным. В зависимости от задачи, одну
и ту же нагрузку можно изобразить по-разному. 9 префиксов передаются в Людмила Фирмаль
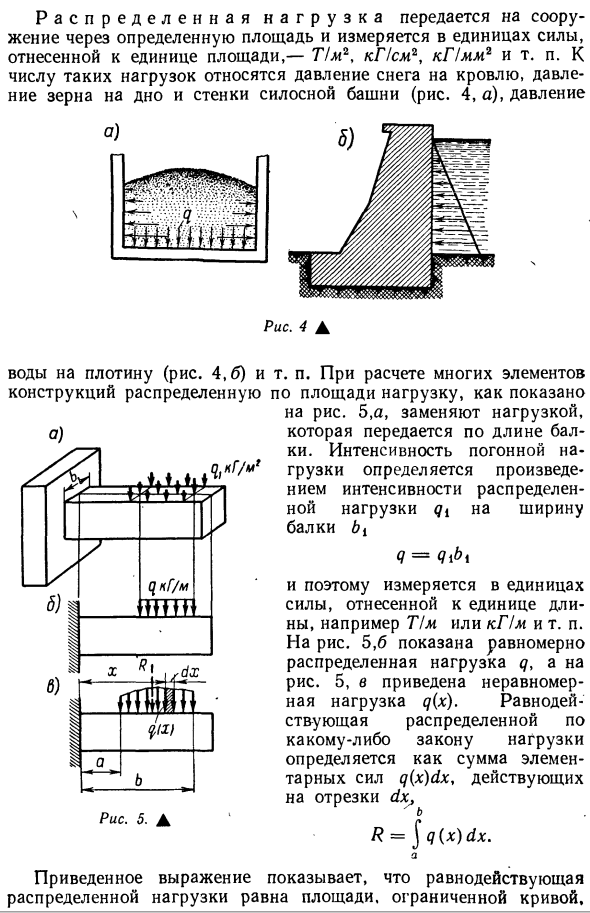
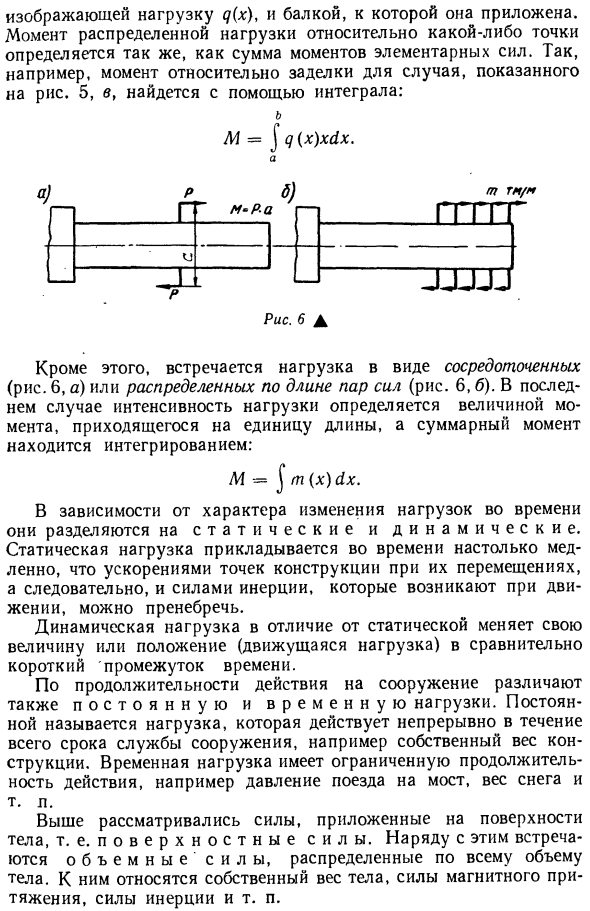
конструкцию через определенные области и измеряются в единицах силы на единицу площади — Т / м \ кг / см2, кг / мм * и т. Д. К таким нагрузкам относятся давление снега на крыше, давление на дно бункера и зернистость стенки (рис. 4, а) и давление. Рис.4 А Вода до плотины (рисунок 4.6). При расчете многих элементов конструкции рисунок 4 5а заменяет нагрузку, передаваемую по длине балки. Линейная сила нагрузки определяется произведением силы
распределенной нагрузки и ширины луча bt. q == qibt Рисунок 5. А Следовательно, оно измеряется в единицах силы на единицу длины, таких как Т / м или кг / м. На фиг.5 и 6 показана нагрузка q, которая равномерно распределена, а на фиг.5с дана неравномерная нагрузка q (x). Результирующая нагрузка, распределенная по закону, определяется как сумма основных сил q (x) dx, действующих на сегмент dx. R = J q (x) d x. Вышеупомянутое уравнение показывает, что результат распределенной нагрузки равен области, ограниченной
- кривой. Показывает нагрузку q (x) и балку, к которой применяется нагрузка 10. Распределенный момент нагрузки для любой точки определяется так же, как и сумма основных моментов силы. Так, например, вы можете найти момент 5c, связанный с концом случая, показанного на рисунке 1, интегрально используя: b M-J q (x) xdx. р б) т тн / м г «» м * ра гггг и ^ ■ 1’JJJ J J Рисунок 6 А Кроме того, нагрузка может быть сосредоточена (рис. 6, а) или распределена по набору длин сил (рис. 6, б). В последнем случае интенсивность нагрузки
определяется величиной момента на единицу длины, а полный момент получается путем интегрирования. M-§m (x) dx. В зависимости от характера изменения нагрузки с течением времени их можно разделить статически и динамически. Поскольку статические нагрузки прикладываются очень медленно во времени, ускорение движущейся структурной точки и, следовательно, сила инерции, создаваемая во время движения, можно игнорировать. В отличие от статических нагрузок, динамические нагрузки меняют свое значение или положение (движущаяся нагрузка)
за относительно короткое время. В зависимости от продолжительности воздействия на конструкцию также проводится различие между Людмила Фирмаль
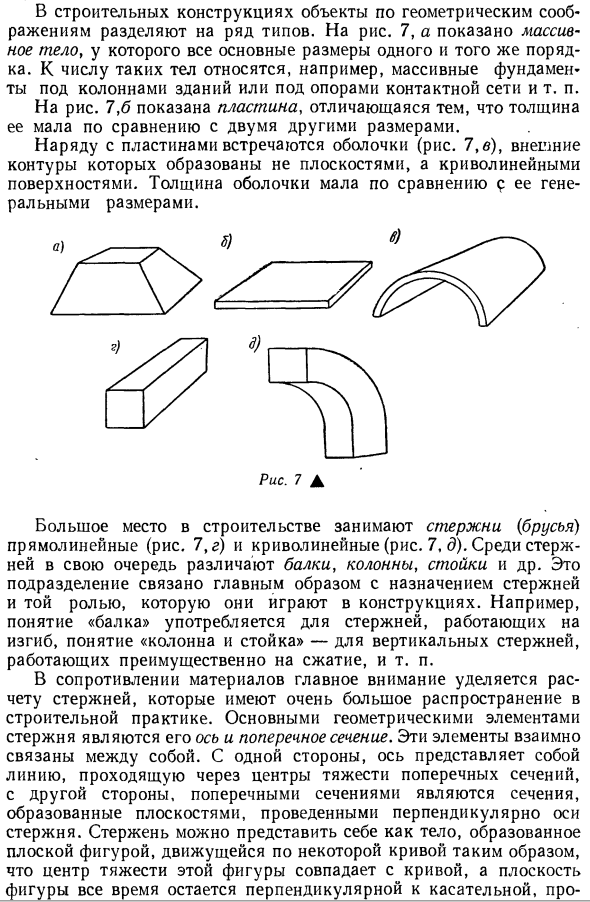
постоянными и временными нагрузками. Постоянная — это нагрузка, которая действует непрерывно на протяжении всего срока службы конструкции, например, постоянная нагрузка на конструкцию. Временные нагрузки имеют ограниченное время работы, например, давление в мостике, вес снега и т. Д. Сила, приложенная к поверхности тела, то есть максимальная сила, была рассмотрена выше. Кроме того, он распределяется в больших количествах по всему организму. К ним относятся масса тела, магнитное притяжение и инерция. В 11 строительных конструкциях объекты делятся на несколько типов по геометрическим причинам. На рисунке 7а
показано огромное тело со всеми основными размерами в одном и том же порядке. К таким органам относятся, например, огромные фундаменты под опорами зданий и при поддержке контактных сетей. На рисунке 7.6 показана пластина, характеризующаяся небольшой толщиной по сравнению с двумя другими размерами. Помимо пластины, существует оболочка (рис. 7, в), внешняя форма которой образована изогнутой поверхностью, а не плоской поверхностью. Толщина корпуса меньше, чем общий размер 9. Рисунок 7 А Большие площади в структуре заняты прямыми (рис. 7, д) и изогнутыми (рис. 7, д) стержнями. В стержне имеются балки, колонны, стойки и т. Д. Этот раскол в основном связан с назначением стержня и ролью стержня в конструкции. Например, понятие «балка» используется для стержней, которые работают с изгибом, а понятие «колонна и колонна»
используется для вертикальных стержней, которые работают в основном со сжатием. В материале сопротивления уделяется внимание расчету стержней, которые очень популярны в основном в строительных работах. Основной геометрический элемент стержня отображается с его осью и поперечным сечением. Эти элементы взаимосвязаны. С одной стороны, ось представляет собой линию, проходящую через центр тяжести поперечного сечения, а с другой стороны, поперечное сечение представляет собой поперечное сечение, образованное плоскостью, перпендикулярной оси стержня. Стержень можно представить как объект, образованный плоской
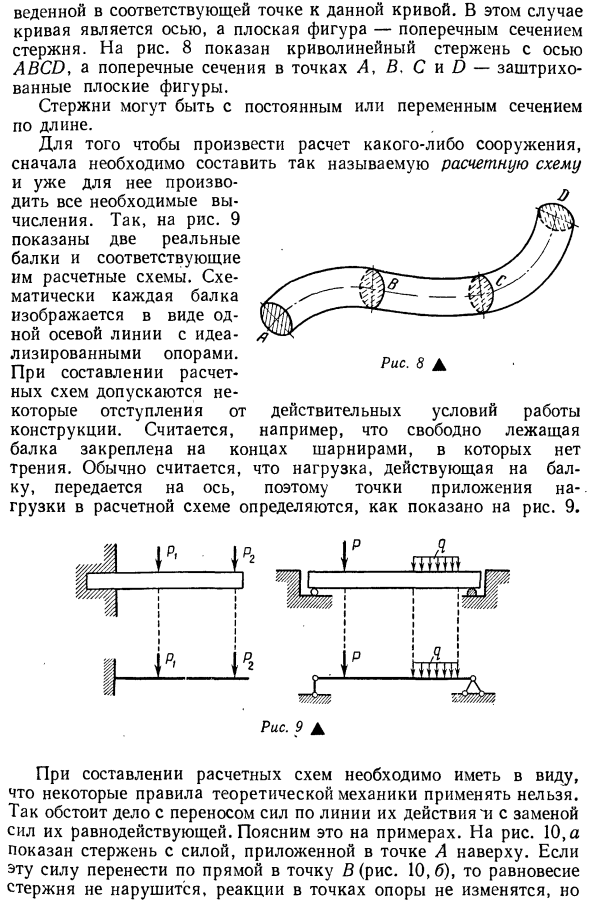
фигурой, которая движется вдоль определенной кривой, так что ее центр тяжести совпадает с кривой, и плоскость фигуры остается перпендикулярной касательной. Дано 12 в точке, соответствующей данной кривой. В этом случае кривая — это ось, а вид сверху — это поперечное сечение стержня. На рисунке 8 показан изогнутый стержень с осью ABCD, а поперечные сечения в точках A, B, C и D являются заштрихованными видами сверху. Стержень может иметь постоянное или переменное поперечное сечение по всей его длине. Чтобы рассчитать структуру, вы должны сначала создать так называемую схему расчета и выполнить все необходимые для этого
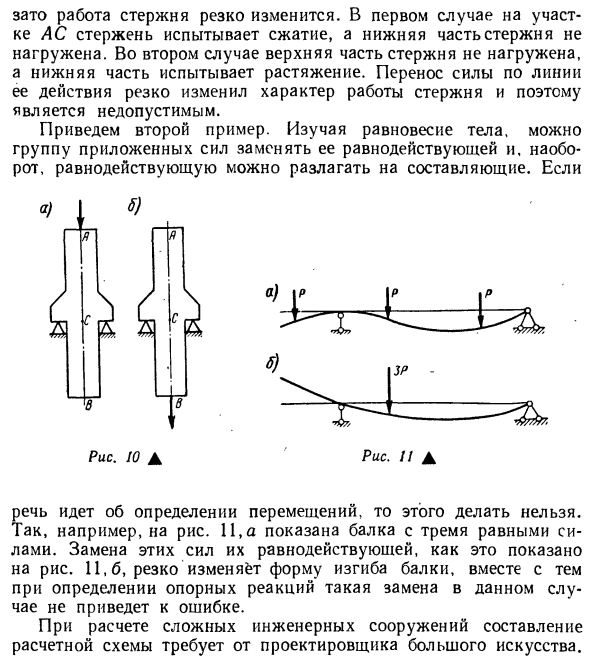
вычисления. Таким образом, на рисунке 9 показаны два реальных пучка и соответствующие им схемы проектирования. Схематически каждый луч изображен в виде единой оси с идеальной опорой. При создании проектной схемы допускаются некоторые отклонения от фактических условий работы конструкции. Например, считается, что свободно стоящий луч фиксируется на обоих концах шарниром без трения. Применение важно, потому что нагрузка, действующая на балку, обычно считается переданной на вал. Расчетная схема
нагрузки определяется как показано на рисунке. 9. При создании расчетной схемы следует отметить, что некоторые правила теоретической механики не могут быть применены. Это случай передачи сил вдоль их действующих сил и замены возникающих сил. Давайте проиллюстрируем это на примере. На фиг.10а показан стержень с силой, приложенной к верхней точке А. Когда эта сила передается по прямой линии в точку B (рис. 10, б), баланс стержня не нарушается и реакция на опоре не меняется, 13 Однако работа стержня резко меняется. В первом случае в области переменного тока стержень сжимается, и к нижней части стержня не прикладывается
нагрузка. Во втором случае нагрузка не прикладывается к верхней части стержня, а натяжение прикладывается к нижней части. Передача силы по линии действия недопустима, поскольку она резко изменила характер работы стержня. Вот второй пример. При проверке баланса тела группа приложенных сил может быть заменена результатом, и наоборот. если Это невозможно, когда речь идет об определении смещения. Так, например, на фиг.11 показана балка с тремя равными силами. Замените эти силы результатом, как показано. Как показано на фиг.11b, это резко меняет форму изгиба балки, но такой обмен в этом случае не приводит к ошибкам в определении отклика опоры. При расчете сложных инженерных сооружений создание проектной схемы требует умения дизайнера.
Смотрите также:

