Оглавление:


Пример определения геометрических характеристик сложного сечения
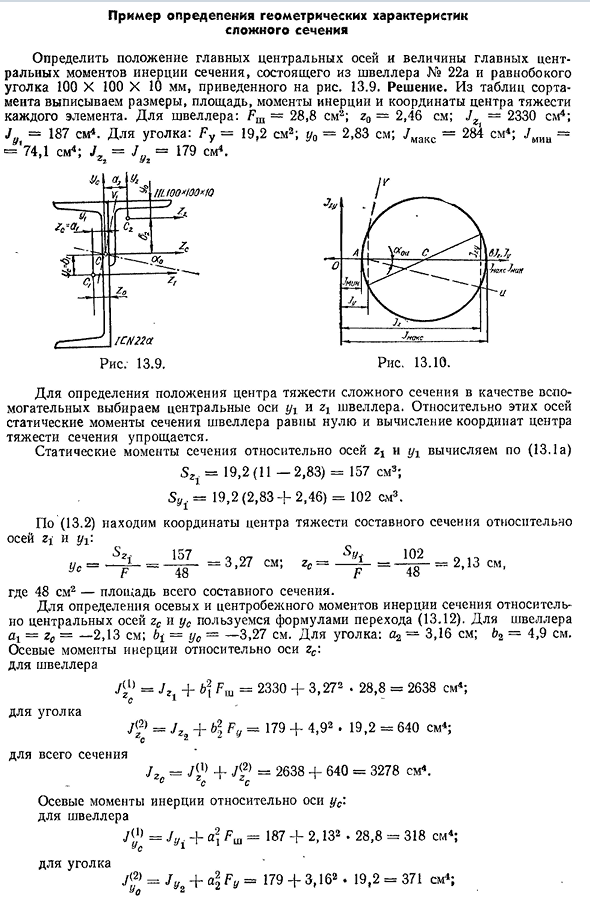
- Пример определения геометрических свойств сложного сечения Как показано на рисунке 22, определите положение главной центральной оси и величину момента центрального центра инерции для секции,
состоящей из канала № 22а и равностороннего угла 100 х 100 х 10 мм. 13.9. Решения. Экспортируйте размер, площадь, момент инерции и координаты центра тяжести каждого элемента
из ассортиментной таблицы. Для каналов: Гш = 28,8 см2; r0 = 2,46 см; Jz = 2330 см4; Jy-187 Людмила Фирмаль
см4. Для углов: Fy = 19,2 см2; ya = 2,83 см; 7max = 284 см4; / mii = = * 74,1 см4; =] год = 179 см4. Чтобы определить местоположение центра тяжести сложного сечения в качестве вспомогательного средства, выберите центральные оси y и g и канал. Для этих осей статический
момент сечения канала равен нулю, и расчет координат центроида сечения упрощается. Статический момент сечения вокруг осей zt и yx рассчитывается по формуле (13.1a) S21 = 19.2 (11-2.83) = 157 см3. Syt = 19,2 (2,83 + 2,46) = 102 см3. По осям rm и yr (13.2): Нас = Найти
- координаты центра тяжести составного сечения 157 48 = 3,27 см; 102 48 = 2,13 см Где 48 см2 — общая площадь составного сечения Формула перехода (13.12) используется для определения осевого направления сечения и центробежного момента инерции относительно центральной оси rf. Для канала a = ge = -2,13 см; Bg = yn = -3,27 см. Для углов: а2 = 3,16 см. B2 = 4,9 см Осевой момент инерции относительно
оси gf: для канала 1) = -j-b2 Flu = 2330 + 3,272 • 28,8 = 2638 см4; для угла ^ -b 2 Фу = 179 + 4,92. 19,2 = 640 см4; Во всем поперечном сечении J 2 = Y <+> / 2) = 2638 + 640 = 3278 см4. s gs g s Осевой момент инерции вокруг оси усов: Канал 7 (1) = Jy. + a2 = 187 + 2, 132 • 28,8 = 318 см4; 1 Для углов / <2 ’= Jy + a2 Fy = 179 4-3, 162. 19,2 = 371 см4; Jyc = / 0) + = 318 + 371 = 689 см * в поперечном сечении 253. Определим центробежный момент инерции относительно оси канала zCt us D ‘) = = (-2,13). (-3,27) • 28,8 = 200,6 см *; C ^ C Для угла r (2) j t „h P ■ ‘max Jmi ,, p = J ^ 2 + a ^ P Y = ——— 2 ———— a ^ F y = 284_ 74 | = 2 ’- + 3.16. 4,9 • 19,2 = 402,2 см *;
Обо всем разделе ! r & = £ = 200,6 + 402,2 = 602,8 см *. Используйте (13.15), чтобы Людмила Фирмаль
определить местоположение главной инерциальной центральной оси поперечного сечения. , „2 • 602,8 _ g 2 «°» 689-3278 ° ‘4 6 6, 2a)) = -25 °; aw = -12 ° 30’ и oi = 102 ° 30 ‘. Рассчитайте главный центральный момент инерции (13.13). ■ ‘max = Ju = -3 2 7 8 + 6 89 + C- / (3 2 7 8 -6 8 9) «+ 4 (602,8 / = 3411 см *; •’ min = СП = —— —————— 2 ~ V (3278-689) 2 + 4 <6®2> 8) 2 = 5 5 5 см 4. Графическое определение основного момента инерции и положения главной оси — построения круга Крота — осуществляется по приведенным выше правилам. На рисунке показана конструкция торгового центра. 10/13.
Смотрите также:
| Круги инерции | Влияние повышенной температуры на механические свойства |
| Эллипс инерции | Влияние скорости испытания |

