Оглавление:



Свободные незатухающие колебания
- Свободная вибрация без демпфирования Упругая система, вызванная силой из положения равновесия после прекращения действия силы,
представляет собой свободную вибрацию или уникальную вибрацию. Простейшая линейная * механическая модель **
вибрационной системы с одной степенью свободы представляет собой массу pg, Людмила Фирмаль
соединенную с пружиной (рис. 10.9, а). Дифференциальное уравнение свободной вибрации системы составляет mz / «+ cz / = 0, (10.27). C — коэффициент жесткости пружины. Массовое движение — это гармоническая вибрация y = A sin ( o — начальное отклонение и
массовая скорость при t = 0. * Линейка — это система, связанная с линейной зависимостью между силой и отклонением или скоростью. ** Число степеней свободы — это всегда число независимых
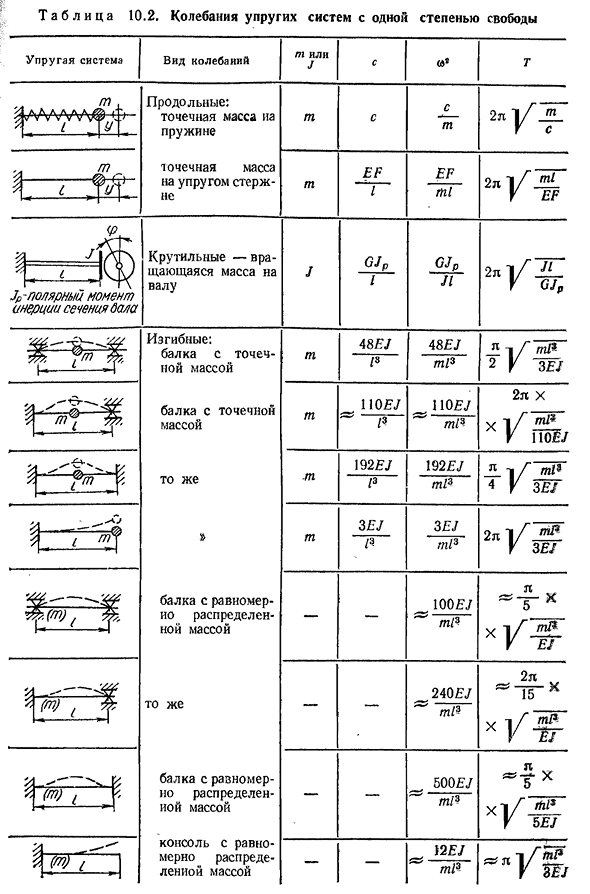
- геометрических координат, определяющих положение всех масс в системе. , J (10.34) 222T a b l i c a 10.2. Вибрация упругой системы с одной степенью свободы S23 (10,35) Начальный этап определяется по
формуле е = Arctan-p-, максимальная суммарная деформация системы Un = Ust + A = Ust = ^ Ust. (10.36) d величина kR = 1 ——- называется динамическим коэффициентом. Здесь статическое отклонение массы рта увеличивается.
Для упругих линейных систем напряжение, возникающее в результате свободной вибрации, определяется как <7d Людмила Фирмаль
= idst. (10.37) В таблице. 10.2 показывает жесткость, собственную частоту и период колебаний нескольких схем линейных систем с одной степенью свободы.
Смотрите также:

