Оглавление:
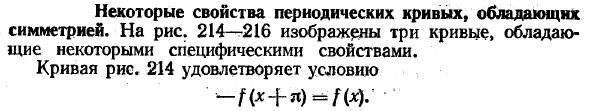

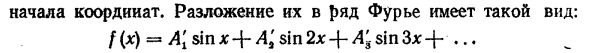

Некоторые свойства периодических кривых, обладающих симметрией
Некоторые свойства периодических кривых с симметрией. На рисунках 214-216 показаны три кривые с определенными свойствами. Кривая 214 удовлетворяет условию -f (* + ”) = f (x).
- Кривая, удерживаемая этим свойством, называется симметричной относительно абсциссы. В случае диаграммы кривая 214 находится вдоль оси x Он должен быть сдвинут на половину цикла и зеркально отражен вокруг оси x,
и результирующая кривая совпадает с кривой f (x). Людмила Фирмаль
Нет даже волны, то есть коэффициент Ao = A ‘= A \ = A’ <= A / = … = 0. Таким образом, кривая в соответствии с типом кривой на рисунке размещена в следующей строке 214 ‘F (x) = L; sin x + L’ ‘cos x L’ sin Zx 4- L ^ soe Zx C- … Рисунок 215
Каждый член этой серии является условием -f (xC-n) => = / (X), так, например, -sin (x 4-l) = sin x, которая является симметричной относительно кривой 215, ордината, аналогичная кривой на фигуре. / (-X) = f (x)
- Если кривая на левой стороне оси ординат отражается относительно оси ординат, результирующая кривая будет соответствовать кривой на правой стороне оси ординат.
Нет синусоидальной составляющей (то есть A ‘/ C = A’ = … = 0), поэтому кривая 215 в зависимости от типа кривой на рисунке помещена в следующую строку F (x) = Lo4-L / cos x 4-L «cos2x 4 ~ L» cosZx 4 ~ ••
только косинус и постоянные составляющие Людмила Фирмаль
Кривая 216 в зависимости от типа кривой обладает свойством -f (-x) = * = f ( х), которые называются симметричными кривыми относительно начала координат, форма разложения в ряд Фурье: f (x) = * A {sin x + D ‘sin 2x sin 3x +. ..
Смотрите также:

