Оглавление:



Расчет по бимоментам
- Двух-моментный расчет Расчет тонкостенных стержней открытого профиля часто основывается на бименто в (9.8) , 211 В этом случае дифференциальное уравнение (9.6) записывается в виде В «-Л = т (9.9).
Две интегральные постоянные, включенные в общее решение, определяются из граничных условий в зависимости от свойств расширения концевого участка стержня.
«= Без схода с рельсов при Людмила Фирмаль
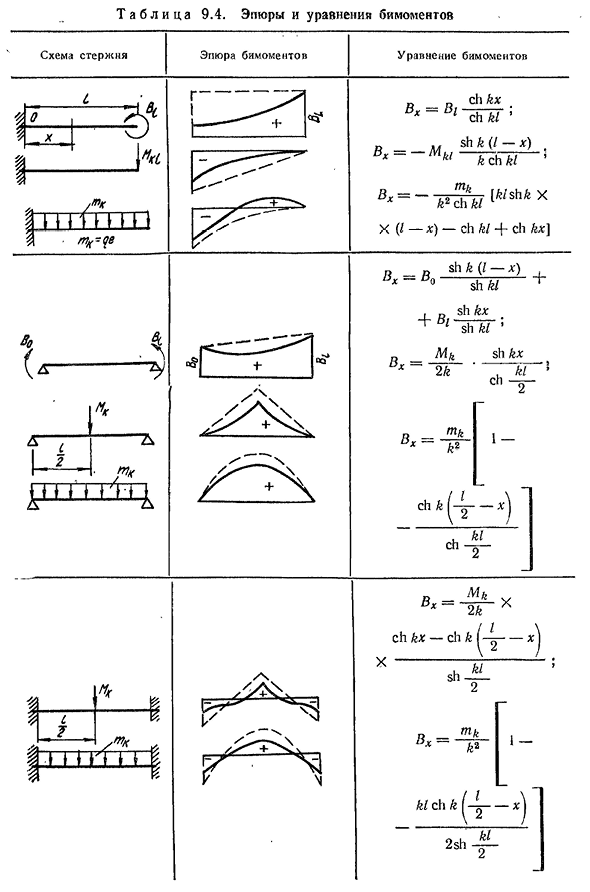
Mk. Уравнения и таблицы гиперболических функций в некоторых случаях приведены в таблице. 9.4. После нахождения и определения крутящего момента изгиба, дБ M (L == ~ yx ~ <9-10) И момент
свободного кручения M0 = Mk-Ma. (9.11) нормальное напряжение из-за бимомента, g d e g o> „ (9,12) Наибольшее значение вы: м акета (9,13) Я т н я л 11 Я \ о! L 0,41 O и Ts21 ” 1 Моменты сопротивления по отделам. (Bonus Сечение x открытого профиля в средней точке с
- координатой дуги s определяется по формуле N Mug, Mgu, F Jy + J2 «(9-14). Первые три слагаемых соответствуют гипотезе плоского сечения, и согласно обычному уравнению материального сопротивления стержней с большой массой поперечного сечения четвертый слагаемый — из ограниченного кручения — равен (9.12)
Будет решено. Соглашение о знаках для всех усилий показано на рисунке 9.4. В разделе bimo ent schi положительный ce, если напряжение oi отрицательное (сжатие), положительное. Напряжение сдвига в сечении из-за изгибающего момента: M S0T От T 0> J J 2) -sh fe (x-1,2) -fe (x-3,6) 4-sh fe (x-3,6)] —
Mek sh fe (х-4,8). 1 (Получить уравнение B = ——— sh k x ——— —— sh fex 4 —— sh fe (x-1,2) — t —— [от h (x-3.6) -h до (x-1.2)] + Me ch fe (x-4.8), k Людмила Фирмаль
Дифференциальная сила с моментом: Л1И = 6361 ч kh-20733 ч kh -f P hkxtnx (x-1,2) ——— w 3,6) -sh fe (x-1,2)] 4- Мек ш фе (х-4,8), фе (9.12), (9.15) на
Смотрите также:
| Механизм хрупкого разрушения | Устойчивость тонкостенных стержней |
| Прочность при низких температурах | Частные случаи |

