Оглавление:




Напряжения при чистом изгибе плоского кривого бруса (м 0, n = 0, q = 0 )
- Чистое напряжение на изгиб Плоская криволинейная балка(M0, N=0, Q=0 ) Предполагается: 1)сечение плоское и плоское к оси балки до деформации остается нормальным и после деформации;2) продольные волокна балки, уравновешенные изгибающим моментом изгиба перпендикулярным уравнением напряжений: M (R—r) Mu°
«(G+y)-FE1«K (7.2) и фиг. 7.3: p-радиус кривизны оси пучка, g-радиус кривизны нейтрального слоя, R-радиус кривизны любого волокна, y-расстояние от нейтрального слоя до исследуемого волокна; Rt и
R2-радиус соответственно внешнего и внутреннего волокон пучка; C- Людмила Фирмаль
центр тяжести — ось кривизны; e=p-g-расстояние от центра масс сечения до нейтральной оси; S=Fe-средняя (7.2) Если ось Y симметрии направлена от центра кривизны, то формула (7.2) дает не только величину, но и знак напряжения. В изогнутой балке нейтральная ось
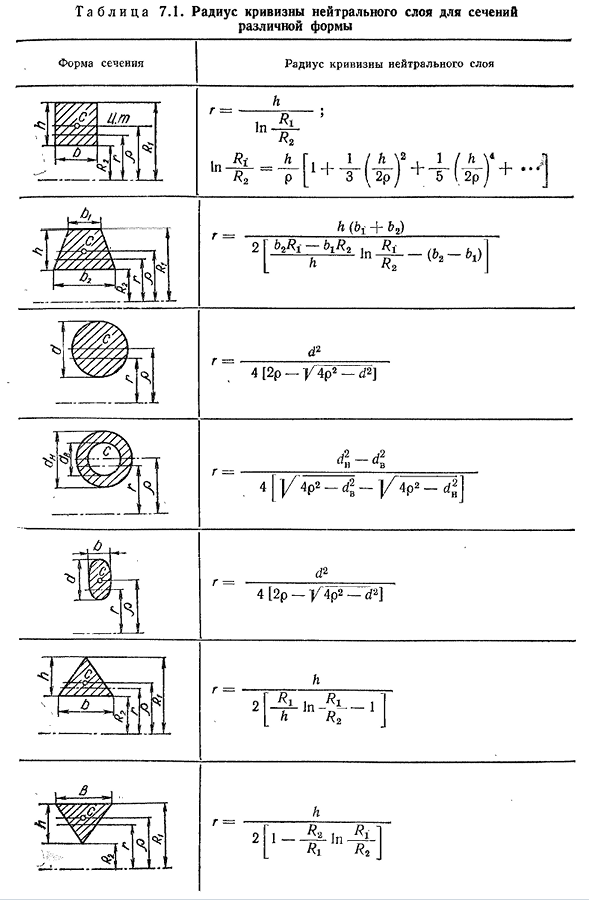
не проходит через центр тяжести сечения, а находится между центром тяжести и центром кривизны (рис. 7.3. — Ось АО). Радиус кривизны нейтрального слоя для любого сечения зависит только от формы сечения и обычно определяется формулой Ф dF R (7.3) 170т
- а б л и Ц А7. 1. Радиус кривизны нейтральной поверхности для различных площадей поперечного сечения велик и требуется формилацетат g. так как формула (7.2) содержит разность между двумя численно близкими значениями R и R, то значение радиуса кривизны нейтрального слоя для некоторых форм сечения можно определить из таблицы e, для наиболее распространенной формы
поперечного сечения кривой стержня 7.1, приведенной в таблице. За столом. Значение коэффициента k задается в зависимости от отношения p/d, где a-расстояние от центра тяжести до крайних волокон внутренней кривизны. Свое поперечное сечение N. N. In в соответствии с Давиденковым[6] значение кривой стержня малой кривизны с двумя осями симметрии е
можно определить с помощью-J Аббревиатура*: Е -, где J-момент инерции сечения относительно центральной оси, параллельной нейтральной линии; Людмила Фирмаль
Р-радиус кривизны оси балки в разделе исследования. Нормальное напряжение на высоте поперечного сечения изменяется по гиперболическому закону(рис. 7.3). Максимальное напряжение обычно возникает на внутренней кривизне балки **: ово= «Напряжение внешней кривизны= М (Р2-Д) Ф р. т-п-р)’ (7.4)) М (рт-г)^(р-г)’ (7.5) *Эта формула также может быть полностью использована в практических целях для симметричных одноосных секций с меньшей точностью. * .В особых случаях, когда центр тяжести сечения очень близок к внутренней кривизне балки, это возможно
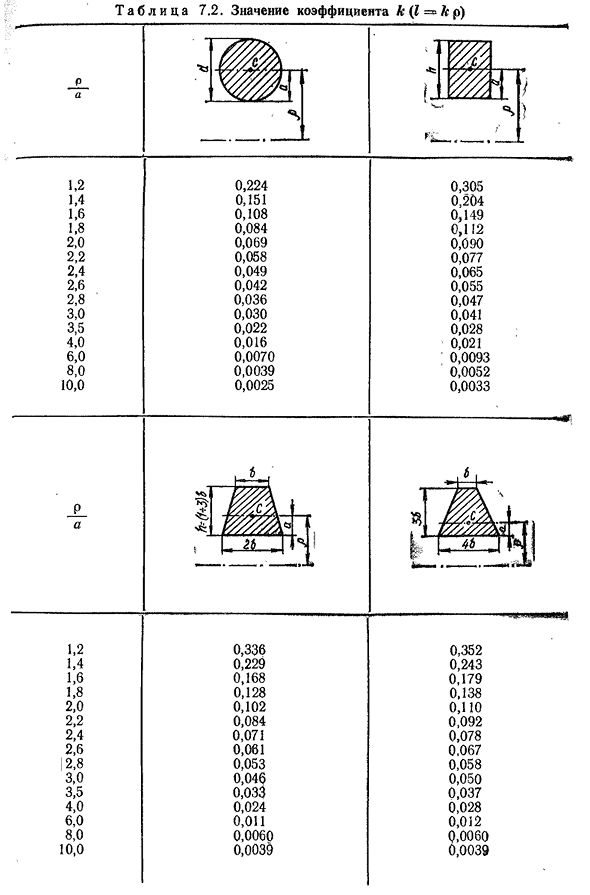
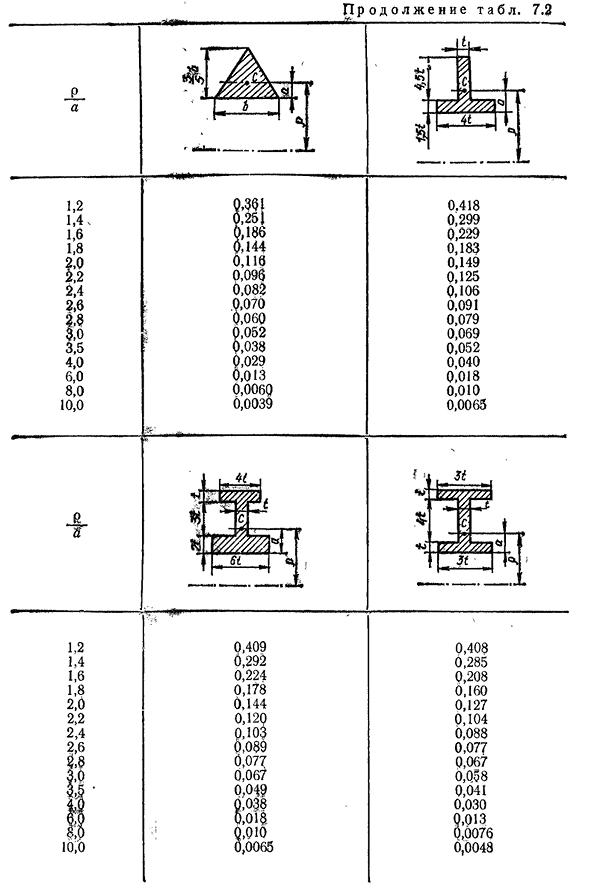
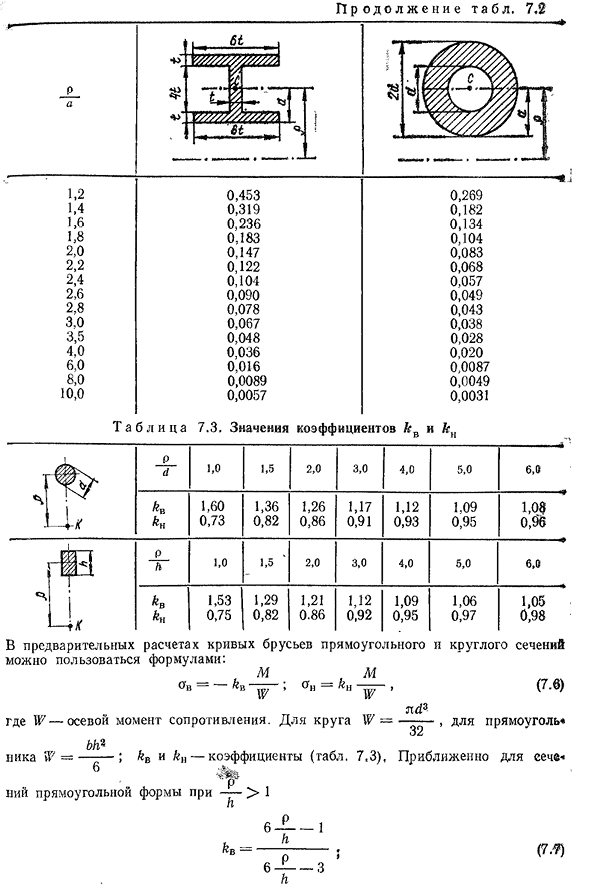
(OI/>] ov/. 172T а б л и Ц А7. 2. Значение коэффициента K (I= = K p) п Но 1,2 0.224 1.4 0.151 1.6 0.108 1.8 0.084 2.0 0.069 2.2 0.058 2.4 0.049 2.6 0.042 2.8 ′ 0.036 3,0 0.030 3.5 0.022 4,0 0.016 6,0 0,0070 8,0 0,0039 10.0 0.0025 0,305 0,204 0.149 0.112 0.090 0.077 0.065 0.055 0.047 0.041 0.028 0.021 0.0093 0.0052 0.0033 < URL-адрес Но Пятнадцать. ■я; 1,2 0,336 1.4 0.229 1.6 0.168 1.8 0.128 2.0 0.102 2.2 0.084 2.4 0.071 2.6 0.061 [2,8] 0.053 3,0 До 0,04(5 3.5 0.033 4,0 0.024 6,0 0.011 8,0 0,0060 10.0. 0. Ноль ноль три§ 0.352 0.243 0.179 0.138 0.110 0.092 0.078 0.067 0.058 0.050 0.037 0.028 0.012 Вопрос: 0060 0.0039174 п р О Д О л ь ш е н и Е Т А Б Л. 7.2 1,2 1.4 1.6 1.8 2.0 2.2 2.4 2.6 2.8 3,0 3.5 4,0 6,0 8.0 10.0 0.453 0.319 Из 0.236 0.183 0.147 0.122 0.104 0.090
0.078 0.067 0.048 0.036 0.016 0.0089 0.0057 0.269 0.182 0.134 0.104 0.083 0.068 0.057 0.049 0.043 0.038 0.028 0.020 0.0087 0.0049 0.0031 Т а б л и Ц А7. 3. Значения коэффициентов LP и KP п Д1,0 1,5 2,0 3,0 4,0 5,0 5,0…… Г 6, авг. 1,60 0.73 1,36 0.82 1,26 0.86 1,17 0.91 1,12 0.93 Из 1.09 0.95 1.0$ 0.9 ′ 6 п футов1.0 1.5 2.0 3.0 4.0 5.0 6,® ч и1. 53 1.29 1.21 1.12 1.09 1.06 1.05 Один. М/г0, 75 0,82 0,86 0,92 0,95 0,97 0,98 при предварительном расчете кривой стержня в прямоугольном и круговом сечениях можно использовать формулу: М, М И — — — — — — КА, (7.В) где 117-осевой момент сопротивления. Для окружности W= В nd3 бит2 Ник 117= ——- ; „b и“
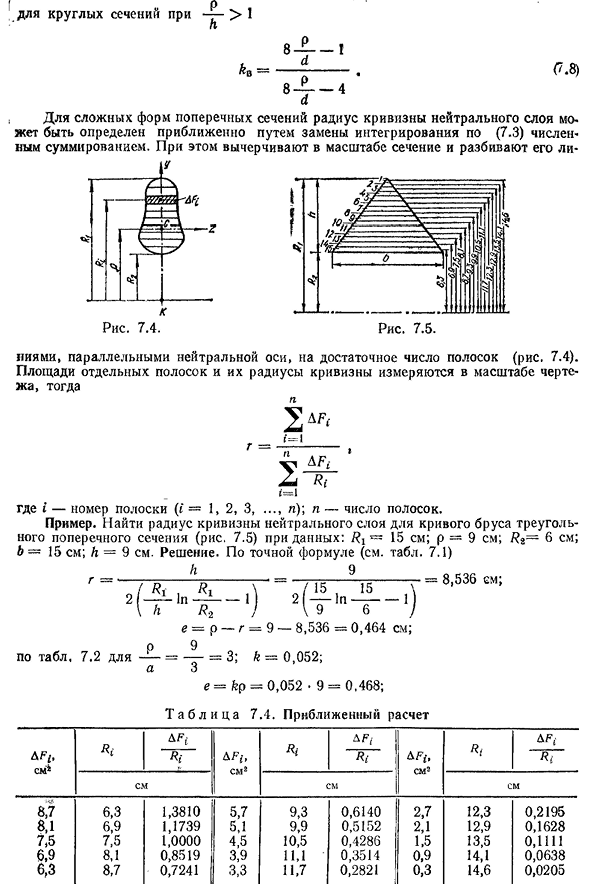
H-коэффициент (табл. 7,3), 6. Прямоугольная форма при->1 Тридцать два. К о поперечном сечении для Бхутто» (7.7) 175(7.8)) Для сложных форм поперечного сечения радиус кривизны нейтрального слоя может быть аппроксимирован заменой интеграла на (7.3). В этом случае нарисуйте поперечное сечение на шкале и разбейте его.- К Рис 7.4. Параллельно нейтральной оси расположено достаточное количество полос (рис. 7.4). Площадь отдельных полос и радиус их кривизны измеряются в масштабе чертежа 2 4Ф< «=1 «’=1 Где i-количество полос(i=1,2,3,…. I); n-количество полосок. Например. Найти радиус кривизны нейтрального слоя для криволинейной балки поперечного сечения треугольника(рис. 7.5)прилагаются: РТ~15см; Р=9см; РС-6 см; б=15 см; Н=9 см. Решение. По точной формуле (см.
табл. 7.1) г=~~ТР—1?——Г=:::~П5 — — — — Л5 — — — -=: = 8,536 ЭМ; 2/ — 2L1H-21—— 1 2( — в— —— 1)\h R2J\9 6}e=p-g=9-8, 536=0,464 см; П9 Согласно таблице, для 7.2 — — — = = = 3; k-0,052;AAE=fep=0,052•9=0,468; T a b l и C a7. 4. Приближенный расчет Д-Р.;, см2 Д-Р.; Д-Р.;, см2 Д-Р.; Д-Р.;, Я, Д-Р.; Я; СМ СМ СМ 1,3810 5,7 6,3 8,7 9,3 12,3 2,7 0,6140 0,2195 8, 1, 6, 9, 1,1739, 5, 9, 9, 5, 9, 5, 2, 2, 12, 9, 0,1628 7,5 7,5 1,0000 4,5 10,5 0,4286 1,5 13,5 0,1111 6.9 8.1 0.8519 3.9 11.1 0.3514 0.9 14.1 0.0638 6.3 8.7 0.7241 3.3 11.7 0.2821 0.3 14.6 0.0205 По формуле 176N. 36J / I2 92 2- » F-=-N—-’=To-=T5n=0.0 cm; FP bhp18P18-9 приближение: разделите треугольник на 15 полос, а затем на высоту 0,6 мм./ Показано на фиг. 7.5 s расчет AF, R (n. расчет производится в табличном виде(табл. 7.4). g= —— = — 61*a=-8.544 см; e=0.456 см. AFZ7 ′ 9 2л Р{
Смотрите также:
| Брусья некруглого сечения | Напряжения при изгибе плоского кривого бруса в общем случае (м =£ о, n =£ о, q ф 0) |
| Основные предпосылки | Деформации кривых стержней |

