Оглавление:






Балки конечной длины на упругом основании
- Теория расчета упругой балки на основе гипотезы Фусса-Винклера применена к методу начальных параметровакадемика A. N. It подробно разработан Крыловым. Преимущество этого метода заключается в том, что уравнение балки на любом типе нагрузки
и упругом основании прогиба y0 в качестве начала координат для любого способа фиксации концов криволинейных осей балки, в случае балки конечной длины на угловом упругом основании Винклера, уравнение является простым. 150т а б л и Ц А5. 20.
Начальные параметры для расчета балки на упругом основании Людмила Фирмаль
Диаграмма направленности Uo0O Alo Qo + Б2+4DtD[а±г-т—- ————КЦ я-Д ТБ Т РЗ Б Ла л-+4С/ДЗ В———————— 5———- * DtBt — 0, 0. Пг с ЛБ л-А-Д ля l_g к-т ф-д и Б Т П п б л б л А-С ла л А К Д М-с Дж 0, 0. У вас есть 717X1711? Б Л’ Ди (Bt_a-Bt_b) — м—(кар-а-Ct_b)к сі СЈ-DtBi КТ (Bi_a-Б(b) — м$. Б я (с[-А кг—Б)~К Д ЖБИ-с Дж 0, 0. P2_I Д лку-А+Б-ля я-к м BtCi-Д / Аи РЗ икмп/_a4-Ag_ai Т, N поужинать-BZCZ 0, 0. P4DzZ)z_a+е zBz_n к Б Б фии-это тд и P2iCiD[_a4-б^я-к Ц/А-я-б ТК Т 0, 0. — Ди — (А^ — А^) — Д-Б Л (Ct_a-Cg_b)^п т б фии-АИДТ~к КТ (Ag_a-а(_b) — В (С, а-Cz_ б) DiAi-
CgBi 0, 0. 4B2B л б л-а-i_a ТС — Л.———————————- к Д2 4-4БЗДЗ 4pa4Dz6z_a+АИБ[а — — — — — — -!— м — — — — к.———— A]4-4BZDZ 0, 0. 4 фута Р 1с1-Д-Л Р / а к ЭйДжей+Abdt 4DiDi_a4-рис^Д? +4fizDz 0, 0. Шесть. Иби_ _ щ+а(л-А-а призраки^к Аль-iBlDi АИ (Pt_a-Д i_b)-4[3(л-АФ-а) к Ал 4-4BZDZ 0, 0. 151 а, П р О Д О Л Е Н И Е Т А Б Л. 5.20 Я Схема пучка UO 0 ″ m » Qo Отчет 403DiA (а-Б fil_a—Т———— • k4Dj+БЖ о-фи» п Но / Отчет < Дквл-а~^ИД Л-Г К Ш И Й+БФ 4Б>; Cz_4-Б; Az_A4D? + БФ 4DtDi_a+BiBl_a Да2 т. + Б2 Ноль. ХД Вт/(с z_a-Cz_ft)++Б а л-А-л-б) 4D2+В2 Ноль. Б и А^ —
- С^)-м-Б>1(Az_a—а/_d2,+bz2, что один Я 0 40-х годов с Филь-А-Д lBt_a к м ИД я-б fli0BiBt_a-AiCt_b Р’ » AjDj-С^ один 0 402c lE>L-a-G Q_O k aidt-B fit Отчет н Бик ф-а-ИД^П А я Д и-б е я т О CI (л^-А/)++4Д [(Di_a-Ди-б)] ди-Биси 0 4Б/(Dz_fl-Dz_b)++л А Л-’ai_b) а фии-б[ди Диаграмма направленности луча.(/о©0Qo С Я С^ — Д т б^б ИД Ай-Си Джей 0м Б/ -, — B0cz_a Б/г — Р с ИД[а-Д fii_o Р ’ BtDi-С2т Сто пятьдесят два. п С fli_a-BiDl_B ИД т-с Дж КЛ(Ал-А-Б+М+4Д з (Ди-Джи-Ди-Джей-б) 402BtDt-с] Икс (Dz_A-Д 4Г;_b)+Би (АЗ-а по б)б ИД Т-С Л А Б Л Я с А5. 21. Функции A, B, C, D и их производные для расчета балок на упругом основании Особенности Производное Один. Два. Три. Четыре. Ах-4 0о Л-4 0 2С — 4 0 3 D, −4 0M, RH04h-4 0 2£>h-4 0 3S — 4º%Sh0vh02L-4 0 3D, −4 0 46h Дуплексный WX^W h0zl-4 0П К K, где ц0,&0, МД, Qо являются исходными параметрами(табл. 5.20);Ах=ch0x
потому Пикс.; ВХ==—(ch0x sin0x ч-sh0x cos0x), СХ= — ш исправить sin0x, ДХ= — (ch0x * Син ПВ-ш РХ Кос) — гиперболические тригонометрические функции (табл. 5.21); f (x)-влияние указанной нагрузки, действующей на балку(табл. 5.22). Исходные параметры некоторых схем крепления балок при любом типе нагрузки представлены в таблице. 5.23 принцип независимости силового воздействия используется для определения начальных параметров сложных интеграционных случаев. Например. Для деревянных балок, лежащих на упругом основании(рис. 5.46), I=4 м, q=2ТС/м, P-4ТС, E=105кгф/см2, поперечное сечение балки b X h=20X20cm3, запишите уравнение коэффициента основания кровати kg=4кгф / см3. Решение. Определение k и 0: k=КГБ=4 *
20=80 кгс / см2; Ф> = / тег=/ ■ л точка= » ■ «» ч г 5.20, запишите начальные параметры: Dt (Bz-B0i5;) (C, — C0i5Z) Ct Использова Людмила Фирмаль
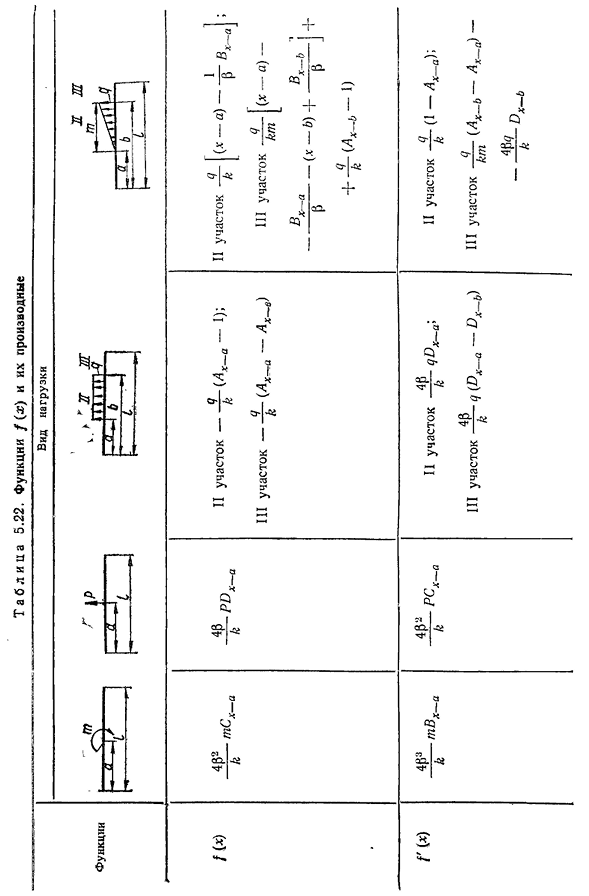
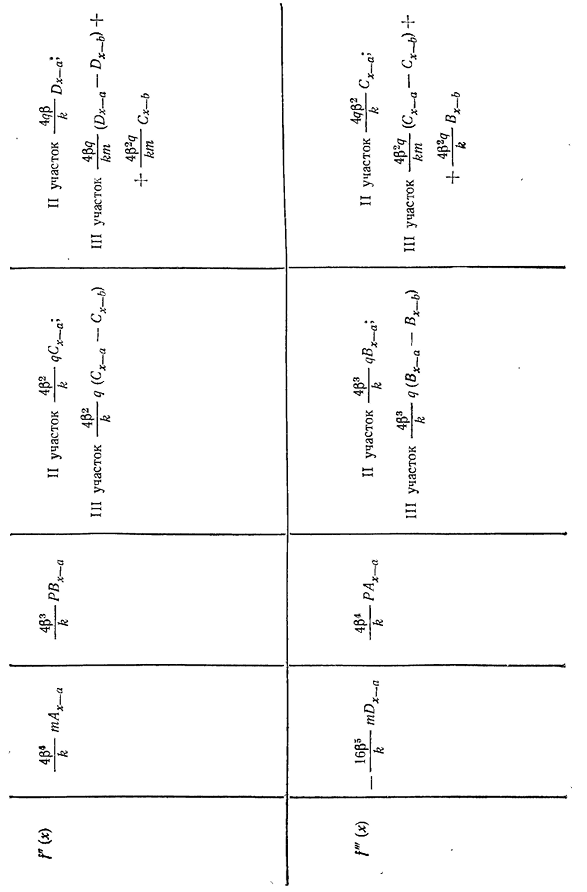
ть таблицу. Uounit Ноль. к 80 * 12 П С/В, С/ — Диао, 31. Qп——;————— — г* * С Л-Д Тбт о Ньютон к р■— —————- т. Замените данные в вопросе C j-d tB t мы получаем: <70 к 0Q Ноль. (5.52) т ф-д-М БЗ (КЛ-с (], 5/) — кл(ПЛ-по 5л) −0.01, 119 см, » £153 Таблица 5.22. Функция f (x) и ее производные Тип нагрузки Особенности Как ttpt4 б Один- Один.. , / 77 , ^Г. ГТ В Главе J7 Доктор Уэллс. Л / ( * ) 4P2g К м кус~в -Это очень, ОЧЕНЬ, ОЧЕНЬ, ОЧЕНЬ, ОЧЕНЬ, — сказал он. II сюжет—— 1-(h-a -!III фаза qk (ah_ и AX_J Второй участок-Д-(х-а)—- — д п; й К Р х-в третий участок-Д — (х-а) — й км в Б х~б х-б и Г Ц<«)+П]++^ — Г и — я ) Г W4P3 ″ к TVX~в Четыре, шесть, двенадцать Р\К~второй участок qDx_a \ III и земельный вопрос(ДХа-Dx_b) II участок (1-Ah_a u, III участок (a^b-Ah__ a> — 4Р? Д к у Х~b4p к 4fl3 к Фаза TT4p2II-qCx_a ; III участок 4P2 к 9(СХ-это СХ-фдж) ТТ 4+ +4kpm3<7^х~б Р w16P5 к 4Р к 4P3 Термин второй qBx_a’
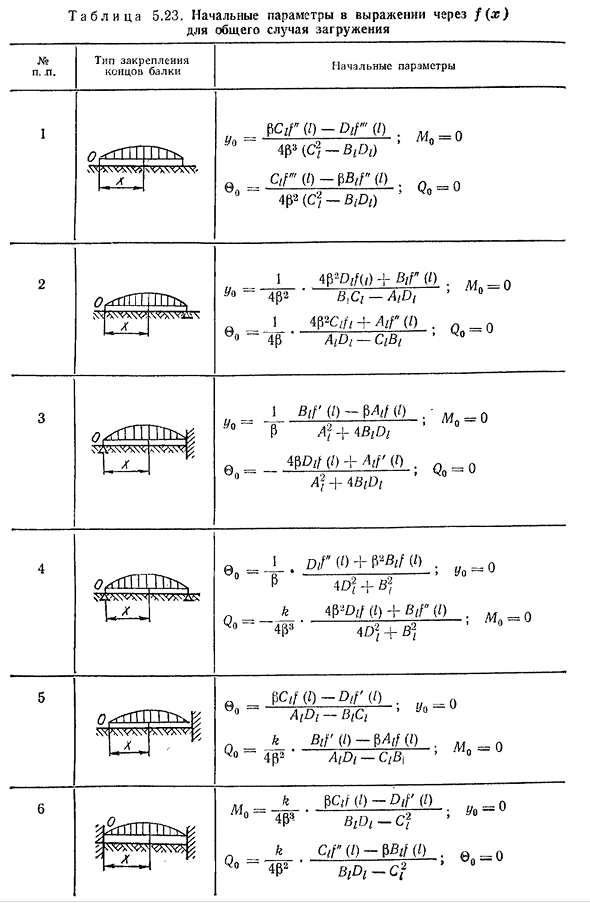
4P3 III участок-q (B x_a-Bx_b ) Т Т4?P2ii plot-Cx_a, III plot(Cx_a-Cx_^+ СТ А Б Л и Ц А5. 23. Начальные параметры выражения f (x) в общем случае нагружения №. Конец луча начальные параметры Н. ’ge. №. ТС (З) — Д ТФ»(я). (ДТ 4fP С2-Б)МО = о Два. Три. Четыре. Пять. Икс С^Гетти, ^\Вт. V х \4Вт Вт! ‘Икс тебя Д0=0 «_ _ ^ Д ИК л)+Биф»(я). M Uo~4^2’s, Q-A/D/ «»-1+a if» Uo o-0 » 4/3 ‘AtD, — CtBi’ Uo 1Б, ТФ(з) — $АТФ (з). — 3А^+м ‘°tyD, если(i)+АТФ'(?)А^+^BtDt ДТФ»(0+м ф/) 4Df+Б2 Qо=° k i^D если(?)+БТФ»(я)4P3 ‘ 4D2+Б2 УО=0 МО=О ПК;/(З) — Д ЗР (з). Айди-Б / ИЦ н _ Btf ±'(я) — МАФ/ф(я). q°~4[32 ‘AiDi-CfBi’ 0~U®0 1/0=0 4/32 ‘е’ -° Шесть. 156 запишите уравнение отклонения на данный момент(5.52) Я Я=о+х+,—/г = -0,2355 Ах-0,01195^ а(1_L)> Я Второй участок-х+0,7/;г=-0,2355 ЛЛ-0,0119 х… я(Ah_^ — ЛВ) 1Вт участок 0,7/х г~ — 0,2 3 5
5 0,0 1 19BZ — — — — — q_(Ax_0i5t-х)-^-р д x_ не^lt, чтобы найти изгибающий момент уравнения, использовать данные в таблице, чтобы выделить уравнение прогиба в два раза и умножим е Ж. 5.21: М х=е и ф=ш е в J0,2355Cz+0,0119 ДХ±1-(Sg_0>5/-с х)-боковой уравнение сил получается, если продифференцировать уравнение изгибающего момента: модель QX=нет. E J0, 2355/D+0,0119^+ -? — (VL0 5/ — B x)—L0J RL. Чтобы построить графики M x и Qx, вы можете вычислить эти значения, задавая значения x через интервалы.
Смотрите также:

