Оглавление:




Расчет бесконечно длинной балки, лежащей на сплошном упругом основании, загруженной одной сосредоточенной силой
- Расчет бесконечно длинных балок, расположенных на сплошном упругом основании, нагруженных одной сосредоточенной силой Если расстояние от конца груза до ближайшего конца превышает 1,5 -^ -, то балка считается бесконечно длинной. Поскольку упругая линия
бесконечно длинной балки симметрична точке приложения нагрузки Р, учитывается половина балки с началом координат в точке приложения нагрузки.
Предполагается, что упругое основание обладает одинаковым сопротивлением как сжатию, так Людмила Фирмаль
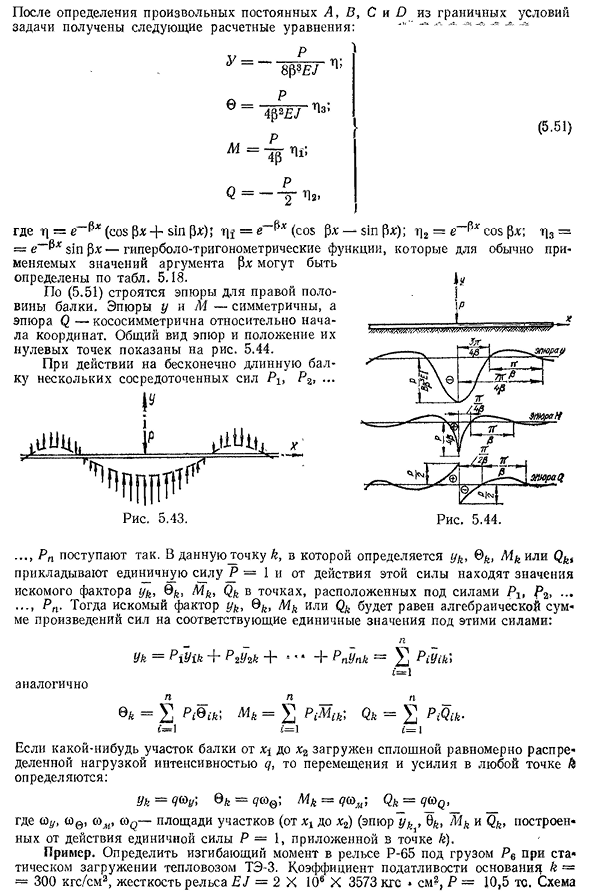
и растяжению(рис. 5.43). В этом случае дифференциальное уравнение изгиба принимает вид: Р У с DXL+ф г=0, (5.49) И его Интеграл г=ае$х Sin модели PX4 ″ ве^х, потому что РХ-Ф-Се — $х Sin Пх Ф-де — $х, потому что. (5.50 )) После определения любых констант A, B, C и D из рассматриваемых граничных условий получаем следующие 147 вычислительных уравнений:’ « » (5-51)) Здесь t|=Е0(со sfJx+грех fjx);
tqj=Б (потому что[на ZX-sinpx); Т]2=е потому что исправить; р]3==е~0грех|3x является гиперболическая функция, значение часто используемых аргументов[DF может быть определена из таблицы]. 5.18. Согласно (5.51)участок строится для правой половины балки. Эпюры м и М симметричны, а эпюра Q является перекос
- симметричного источника. Общий вид участка и расположение его нулевых точек показаны на рисунке. 5-44 При действии на бесконечно длинный пучок некоторой сосредоточенной силы Plt P 2,… …П-п-так. В даннуюточку k, определяемую Yk, M k или Qk, я прикладываю единичную силу p=1,и от действия этой силы находим значение искомого коэффициента yk, 0fe, M k, Qk под действием силы p = 1… …P, p. тогда искомые коэффициенты yk, 0fe,
Mk или Qk будут равны алгебраической сумме произведения сил для соответствующих единичных значений этих сил: N UK=p ivikk+•+Rguk+ * + RPUP/g-Ruia Г=1 Аналогично п п п=С П&П=£П им ИК -,=£ПВК ИК. Если 1=1 1=1i=любая часть пучка от 1x до x2 подвергается непрерывной равномерно распределенной нагрузке интенсивности q, то вычисляется смещение и смещение в любой точке A.: UK=I>u’, 0fe=<7W@:M k=qaM -, Qk=qaQ, где ta0, o>m, O q-площадь участка (от xt до x2) (y k, 0^, M K и Qk построены, а действие единичной силы P-1 приложено в точке k Например.
Определить изгибающий момент рельса Р-65 под статической нагрузкой нагрузки Р6 Локомотива Тэ-3. Коэффициент соответствия: k= = 300kgf / SMA, жесткость рельса Людмила Фирмаль
E J=2X106X3573kgf * cm?, Р-10.5 ТК. Схема 148Т а б л и Ц А5. 18. C), t) h, I функция Чинить П ’1С / РН / Б Px0, 0 1,0000 0,0000 1,0000 1,0000 0,0 0,1 0,9907 0,0903 0,8100 0,900 0,1 0.2. 0.9651. 0.1627. 0.6398. 0.8024. 0.2. 0,3 0,9267 0,2189 0,4888 0,7077 о, З0, 4 0,8784 0,2610 0,3564 0,6174 0,4 0.5 0.8231 0.2908 0.2415 0.5323 0.5 0,6 0,7628 0,3099 0,1431 0,45 0,6 0,7 0,6997 0,3199 0,0599 0,3708 0,7 1 / 4L0. 6448 0.3224 0.000 0.3224 0.785 0,8 0,6354 0,3223-0,0093 0,3131 0,8 0,9 0,5712 0,3185-0.0657 0,2527 0,9 1.0 0.5083 0.3096-0.1108 0.1988 10 1,1 0,4476 0,2967-0,1457 0,1510 1,1 1,2 0,3899 0,2807-0,1716 0,1091 1,2 1,3 0,3355 0,2626-0,1897 0,0729 1,3 1,4 0,2849 0,2430-0,2011 0,0419 1 4 1,5 0,2384 0,2226-0,2068 0,0158 1,5 1 / 2L0,2079 0,2079-0,2079 0,0000 1,571 1,6 0,1959 0,2018-0,2077 0,0059 1 6 1,7 0,1576 0,1812-0,2047
0,0235 1,7 1,8 0,1234 0,1610-0,1985 0,0376 1,8 1,9 0,0932 0,1415-0,1899 0,0484 1 9 2,0 0,0667 0,1231-0,1794 0,0563 2 О2 1 0,0439 0,1057-0,1675 0,0618 2,1 2,2 0,0244 0,089 6-0,1548-0,0652 2 2 2,3 0,0080 0,0748-0,1416-0,0668 2,3 3 / 4jr0,0000 0,0670 −0,1340 −0,0670 2,356 2,4 −0,0056 0,0613 −0,1282 −0,0669 2,4 2,5-0,0166 0,041-0,1149-0,0658 2,5 2,6-0.0254 0,0383-0.1019-0,06,2,6-мне очень жаль. 2,7-0,0320 0,0287-0,0895-0,0608 2,7 2,8-0,0369 0,0204-0,0777-0,0573 2,8 2,9-0,0403 0,0132-0,0666-0,0534■2,9 3,0-0,04226 0,00703-0,05632-0,04929 3,0 3,1-0,04314 0,00187-0,04688-0,04501 3,1 ДжейТи-0,04321 0,00000-0,04321-0,04321 3,142 3,2-0,04307-0,00238-0,03831-0,04069I9 3,3-
0,04224-0,00582-0,03060-0,03642 с;§ 3,4-0,04079-0,00853-0,02374-0,03227 3,4 3,5-0,03887-0,01059-0,01769-0,028,5 3,6-0,03659-0,01209-0,01241-0,02450 3,6 3.7 -.03407-001310-0. 00787-0. 02097 3.7 3,8-0,03138-0,01369-0.00401-0,01770 3 8 3,9-0,02862-0,01392-0,00077-0,01469 3,9 5 / 4Л-0,02786 −0,01393 0,00000 −0,01393 3,927 4,0 −0,02583 −0,01386 0,00189 −0,01197 4.0 4,1-0,02309-0,01356 0,00403-0,00953 4,1 4,2-0,02042-0,01307 0,00572-0,00735 4 2 4,3-0,01787-0,01243 0,00699-0 00544 4,3 4,4-0,01546-0,01168 0,00791-0,3377 4,4 4,5-0,01320-0,01086 0,00852-0,00234 4,5 4,6-0,01112-0,00999 0,00786-0,00113 4 6 4,7-0.00921-0,00909 0,00898-0,000011 4.7 6/4 1-0. 00898-0. 00898 0.00898 0.008000 4,712 4,8-0.00748-000892 0,00892 0,00072 4,8 4,9-0.00593-0.00732
0,00870 0,00139 4,9 5.0-0.00455-0.00646 0.00837 0.00191 5.0 5.1-0 00334-0, 00564 0,00795 0,00230 5.1 5,2-0.00229-0,00487 0.00746 0.00259 5 2 5,3-0.00139-0,00415 0,00692 0,00277 5,3 5,4-0,00063-0.00349 0,00636 0,00287 5,4 7 / 4L0,00000 −0,00290 0,00579 0,00290 5,498 5,5 0,00001 −0,00288 0,00578 0.00290 5.5 5,6 0,00053-0,00233 0,00520 0,00287 5.7 0.00095-0.00184 0.00464 0.00279 5.7 5,8 0,00127-0.00141 0,00409 0,00268 5,8 5.9 0.00152-0.00102 0.00356 0.00254 5.9 6.0 0.00169-0,00069 0.0307 0.00238 6.0 6.1 0.00180-000069 0.00261 0.00221 6.1 6,2 0,00185-0,00017 0,00219 0,00202 6 9 8 / 4L0. 00187 0.00000 0.00187 0.00187 6.283 6.3 0.00187 0.00003 0.00181 0.00184 6.3 6.4 0.00184 0.00019 0.00146 0.00165 6.4 6.5 0.00179 0.00032 0.00115 0.00147
6.6 0.00172 0.00042 0.00087 0.00129 6.6 6,7 0,00162 0,00050 0,00063 0,00113 6,7 6.8 0.00152 0.00055 0.00042 0.00097 6.8 149П Р О Д О л ь ш е н и Е Т А Б Л. 5.18. (5л П ■В х ньютон» 6.9 0.00141 0.00058 0.00024 0.00082 6.9 7.0 0.00129 0.00060 0.00009 0 00069 7.0 9 / 4L0. 00120 0.00060 0.00000 0.0060 7.069 Как использовать 5.45. Триста. 4•2. 10Е три тысячи пятьсот семьдесят три 1_ _ _ _ 1 100 см. К точке приложения нагрузки Pb прикладывают единичную силу p=1, и от действия этой силы необходимо построить момент M, во всех точках которого приложен центр пункта 5.19. Точка X, см i¾ * J’L1P, TS j M, TEM Шесть. Ноль. 0 1, 0000 10. 5 2,625 5 210 2,1-0,1675 10.5-0,440 7 417 4.17 0.0052 10.5 0.0137 4 420 4.20 0.0057 10.5 0.0150 8 627 627 0,0019 10,5 0,0000 9 837 8.37 до 10.5 0,0000 0,0000 3 860 8,60 — 10,5 — 2 1070 10,70 — 10,5 — 10 1277
12,77 — 10,5 — 1 1280 12.80.80 10,5 — 11 1487 14,87 — 10,5 — 12 1697 16.97 10.5 Повышенная интенсивность. Используя таблицу, предположим P=I и выделим точку 6 и (5.51) начало координат. 5.18 выполните расчет. Результаты этих расчетов сведены в таблицу. 5.19 Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р Р С г и Т ф Пять. Пять. 7TK в IE10 он 2/0 2/0 2/0 210 2/0 \ 2/0 № 2/0 2/0 5.45. Момент от нагрузки, приложенной на расстоянии 8 м и более, мал и может быть проигнорирован. Требуемое время работы секции под нагрузкой Pb равно сумме времени, вызванного всеми нагрузками: L46-ям=2,2187 тема. Наибольшее нормальное напряжение на железной дороге, вызванных
Смотрите также:
| Главные оси инерции и главные моменты инерции. | Балки конечной длины на упругом основании |
| Наибольшее и наименьшее значения центральных моментов инерции | Бесконечно жесткая балка на упругом основании |

