Пример №23.
В табл. 5.1 показано оптимальное решение следующей ЗЛП:
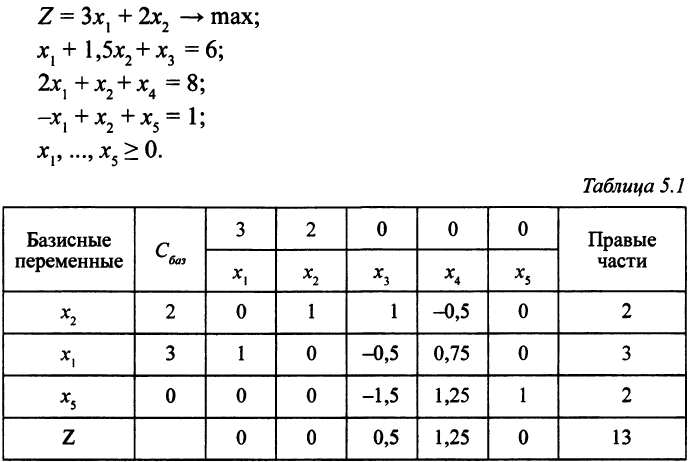
Приведем математическую модель двойственной задачи.
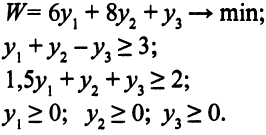
Здесь
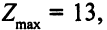
оптимальные значения переменных:
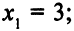
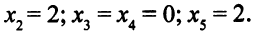
Исходные матрицы коэффициентов при переменных и столбец правых частей таковы
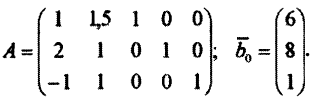
Обозначим через 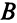 матрицу (часть матрицы
матрицу (часть матрицы 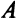 ), столбцы которой — это коэффициенты при базисных переменных данной стандартной формы в исходной системе уравнений.
), столбцы которой — это коэффициенты при базисных переменных данной стандартной формы в исходной системе уравнений.
В случае табл. 5.1. матрица 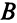 составляется из столбцов коэффициентов при переменных
составляется из столбцов коэффициентов при переменных 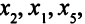 которые являются базисными в оптимальном решении (
которые являются базисными в оптимальном решении (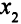 — базисная переменная первого уравнения,
— базисная переменная первого уравнения, 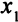 — второго,
— второго, 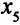 — третьего). Значит,
— третьего). Значит,
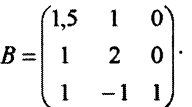
Легко проверить, что обратной матрице 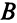 является матрица
является матрица
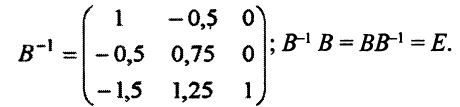
Обозначим через  матрицу коэффициентов системы ограничений из некоторой симплекс-таблицы. В частности, в случае табл. 5.1 имеем
матрицу коэффициентов системы ограничений из некоторой симплекс-таблицы. В частности, в случае табл. 5.1 имеем
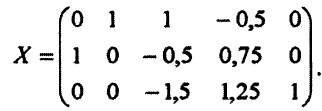
Обозначим через  вектор правых частей, соответствующий матрице
вектор правых частей, соответствующий матрице  . В нашем случае
. В нашем случае 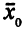 = (2, 3, 2). Матрица
= (2, 3, 2). Матрица 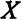 и вектор
и вектор 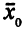 —ото результат умножения матрицы
—ото результат умножения матрицы 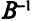 на матрицу
на матрицу 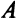 и вектор
и вектор  соответственно:
соответственно:
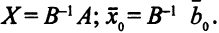
Для рассматриваемого примера получаем
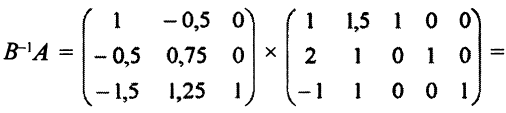
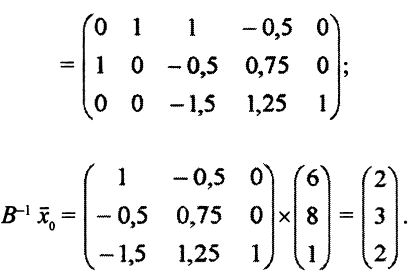
Обозначим через вектор коэффициентов целевой функции при базисных переменных, через 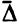 — вектор оценок переменных (
— вектор оценок переменных (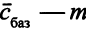 -мерный вектор,
-мерный вектор, 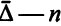 -мерный вектор). Из формул пересчета оценок
-мерный вектор). Из формул пересчета оценок 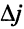 следует, что
следует, что 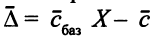 . Так как
. Так как 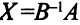 , то
, то
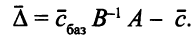
Обозначим через 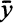 вектор
вектор 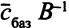 тогда условие (5.6) запишется в виде
тогда условие (5.6) запишется в виде 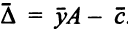 . Транспонируя это равенство, получаем
. Транспонируя это равенство, получаем
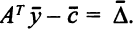
Если 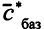 — это вектор коэффициентов целевой функции при оптимальных базисных переменных, то соответствующий вектор
— это вектор коэффициентов целевой функции при оптимальных базисных переменных, то соответствующий вектор 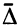 — неотрицателен, все оценки
— неотрицателен, все оценки
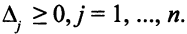
Тогда вектор
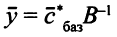
есть допустимое решение задачи (5.4), так как
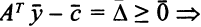
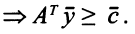
В нашем случае
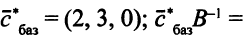
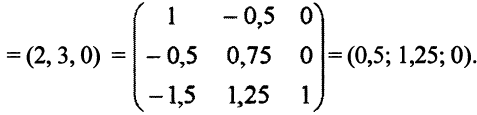
Из равенства (5.7) следует, что оценка 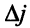 — это разность между значениями левой и правой части
— это разность между значениями левой и правой части 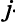 -го ограничения задачи (5.4), когда в качестве значений неизвестных берутся компоненты вектора
-го ограничения задачи (5.4), когда в качестве значений неизвестных берутся компоненты вектора 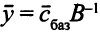 . Эти значения удовлетворяют системе ограничений задачи (5.4) в случае выполнения (5.8).
. Эти значения удовлетворяют системе ограничений задачи (5.4) в случае выполнения (5.8).
Убедимся, что вектор 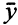 = (0,5; 1,25; 0) — допустимое решение двойственной задачи:
= (0,5; 1,25; 0) — допустимое решение двойственной задачи:
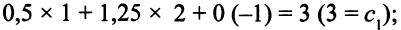
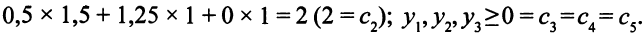
Целевая функция двойственной задачи равна на векторе 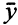 = (0,5; 1,25; 0) числу
= (0,5; 1,25; 0) числу
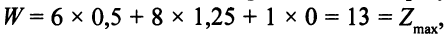
так что найденное решение двойственной задачи не только допустимо, но также и оптимально.
Докажем, что всегда вектор (5.8) есть оптимальное решение задачи (5.4).
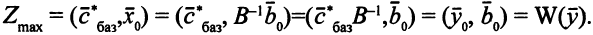
Из совпадения значений целевых функций пары двойственных задач вытекает (следствие 1 из основного неравенства) оптимальность вектора 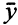 . Теорема доказана.
. Теорема доказана.
Легко видеть, что если исходная система ограничений записана в стандартной форме (матрица 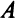 содержит единичную матрицу
содержит единичную матрицу 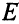 ), то матрица
), то матрица 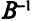 состоит из тех столбцов оптимальной симплекс-таблицы, которые соответствуют исходным базисным переменным. Тогда вектор у составляют оценки этих переменных, сложенные с соответствующими коэффициентами целевой функции.
состоит из тех столбцов оптимальной симплекс-таблицы, которые соответствуют исходным базисным переменным. Тогда вектор у составляют оценки этих переменных, сложенные с соответствующими коэффициентами целевой функции.
В нашем примере переменные 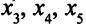 были исходными базисными переменными. Поэтому матрица
были исходными базисными переменными. Поэтому матрица 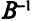 состоит из столбцов оптимальной симплекс-таблицы при переменных
состоит из столбцов оптимальной симплекс-таблицы при переменных 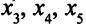 . Оценки этих переменных таковы:
. Оценки этих переменных таковы:
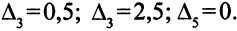
Так как
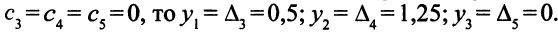
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
| Пример №20. Построить задачу, двойственную следующей ЗЛП |
| Пример №21. Любую ЗЛП можно привести к каноническому виду |
| Пример №24. Рассмотрим такую ЗЛП |
| Пример №24.2. Найти оптимальное решение ЗЛП |

