Оглавление:


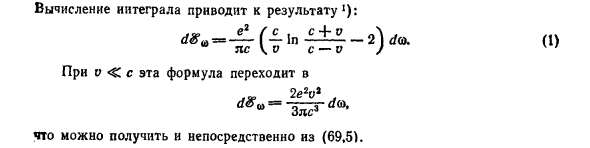

Тормозное излучение малых частот
- Тормозное излучение малых частот. Рассмотрим низкочастотный «хвост» спектрального распределения тормозного излучения. Это область, где большая часть излучения сконцентрирована в области низкой частоты (обозначенной cjq) по сравнению с этой частотой. si <^ sio. (69,1)
Кроме того, как и в предыдущем разделе, мы не предполагаем, что скорость сталкивающихся частиц мала по сравнению со скоростью света. Следующая формула действительна на любой скорости: нерелятивистски Случай luq ~ 1 / m, где m — порядок непрерывного размера Столкновение sti: в суперрелятивистском случае luq пропорционально квадрату энергии испускаемой частицы
существенно ненулевое только в промежутки времени порядка Людмила Фирмаль
(см. §77 ниже). С интегральной о H W = [H eiujtdt — Я Поле излучения H 1 / cjq. Следовательно, при условии (69.1) при интегрировании out <C1, Таким образом, блок Elujt может быть заменен. тогда — Я Теперь подставьте H = [Ap] / s и запустите интеграцию
Время, мы получаем Hw = i [(A 2-A 1) n], (69,2) и Где A 2-A i — изменение векторного потенциала поля, создаваемого сталкивающимися частицами во время столкновения. Подставляя (69.2) в (66.9), общее излучение при столкновении (частота ω) dS’nuj = — ^ 2 [(A2-A i) n] 2 дуэт. (69,3) 4 с7Г Для векторных потенциалов представление можно использовать в виде
- Лиенарда-Вихерта (66.4). д ^ = -4тг! 2hC3; \ {^> Y 4 \ 1 —- t (rlr / c <) — nV-2 —— l —- (lГ / Тc) ^ n — vi) / JY do <lw, ‘ (V 69.4) ‘ Где Vi и V2 — скорости частиц до и после рассеяния, а сумма получается для обеих сталкивающихся частиц. Отметим тот факт, что мы обнаружили, что коэффициент dco не зависит от частоты.
Другими словами, на низких частотах (условие (69.1)) Спектральное распределение излучения не зависит от частоты. Другими словами, dS’nw / dw имеет определенный предел, такой как ω-> O1. Когда скорость сталкивающихся частиц мала Затем введите (69,4) со скоростью света dS, «о, =« Vl’n]) dodbj. (69.5)
Интересный случай применения ранее полученного выражения Генерирует излучение Людмила Фирмаль
Это уравнение соответствует дипольному излучению, а его векторный потенциал определяется уравнением (67.4). , возникающее в результате высвобождения новых заряженных частиц (например, когда /
3 частицы выходят из ядра). В этом случае процесс следует рассматривать как мгновенное изменение скорости частицы — от нуля до его заданного значения (из-за симметрии уравнения (69.5) относительно перестановок Vi и V2), излучение, генерируемое этим процессом, составляет ,
В соответствии с излучением, связанным с противоположным процессом — мгновенной остановкой частицы). Поскольку «время» этого процесса составляет m-> 0, обычно важно, чтобы условие (69.1) действительно выполнялось на всех частотах 2).
Оспаривать Определить спектральное распределение полного излучения в результате излучения заряженных частиц, движущихся со скоростью v. Решения. Согласно уравнению (69.4) V2 = v, vi = = 0, имеем 7G 2 2 4tg V y (1- (v / c) cos c) 2 Интегральный расчет приводит к результату 1: dЈ, u = — (-) n-2) du>. (1) 7ГС «В С-В» Для v с этим выражением dЈ „= d u, 37G C (69.5) можно получить напрямую.
Смотрите также:
| Дипольное излучение | Излучение при кулоновом взаимодействии |
| Дипольное излучение при столкновениях | Квадрупольное и магнитно-дипольное излучения |

