Для связи в whatsapp +905441085890

Определить напряженность EA и потенциал  A электростатического поля в точке А, расположенной вдоль прямой.

🎓 Заказ №: 21974
⟾ Тип работы: Задача
📕 Предмет: Физика
✅ Статус: Выполнен (Проверен преподавателем)
🔥 Цена: 149 руб.

👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.

➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.

➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.

⚡ Условие + 37% решения:

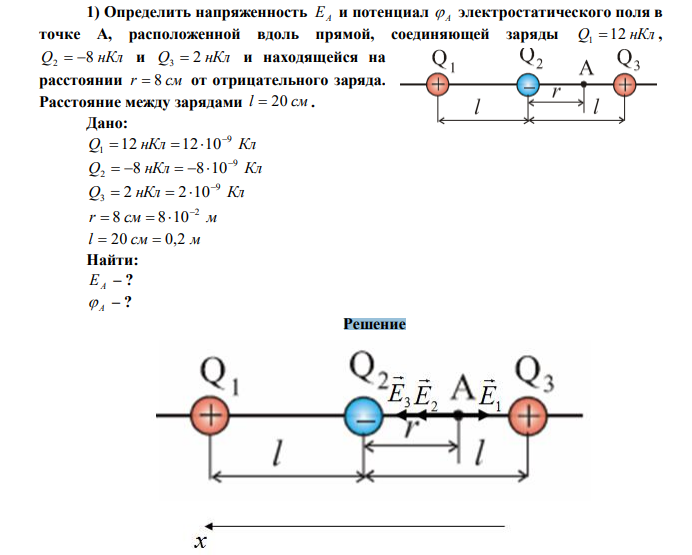
Определить напряженность EA и потенциал  A электростатического поля в точке А, расположенной вдоль прямой, соединяющей заряды Q 12 нКл 1  , Q 8 нКл 2   и Q 2 нКл 3  и находящейся на расстоянии r  8 см от отрицательного заряда. Расстояние между зарядами l  20 см.

Решение Линии напряженности электрического поля направлены от положительного заряда и до отрицательного заряда. В точке A заряд Q1 создает электрическое поле напряженностью E1  , заряд 2 q – электрическое поле напряженностью E2  , а заряд Q3 – электрическое поле напряженностью E3  . Согласно принципу суперпозиции, можем записать: EA E1 E2 E3        Запишем это уравнение в проекции на ось x : EA  E2  E3  E1 (1) Запишем выражение для модуля напряженности электрического поля, созданного точечным зарядом Q : 2 4 0 r Q E   (2) где 12 0 8,85 10    Ф/м – электрическая постоянная;  – диэлектрическая проницаемость среды, в которой находится заряд; r – расстояние от заряда до данной точки. Исходя из (2), запишем выражение для определения напряженности E1 , учитывая, что расстояние от заряда Q1 до точки A равно l  r :   2 0 1 1 4 l r Q E    (3) Исходя из (2), запишем выражение для определения напряженности E2 : 2 0 2 2 4 r Q E   (4) Исходя из (2), запишем выражение для определения напряженности E3 , учитывая, что расстояние от заряда Q3 до точки A равно l  r :   2 0 3 3 4 l r Q E    (5)

Определить напряженность EA и потенциал  A электростатического поля в точке А, расположенной вдоль прямой, соединяющей заряды Q 12 нКл 1  , Q 8 нКл 2   и Q 2 нКл 3  и находящейся на расстоянии r  8 см от отрицательного заряда. Расстояние между зарядами l  20 см.
Определить напряженность EA и потенциал  A электростатического поля в точке А, расположенной вдоль прямой, соединяющей заряды Q 12 нКл 1  , Q 8 нКл 2   и Q 2 нКл 3  и находящейся на расстоянии r  8 см от отрицательного заряда. Расстояние между зарядами l  20 см.
Определить напряженность EA и потенциал  A электростатического поля в точке А, расположенной вдоль прямой, соединяющей заряды Q 12 нКл 1  , Q 8 нКл 2   и Q 2 нКл 3  и находящейся на расстоянии r  8 см от отрицательного заряда. Расстояние между зарядами l  20 см.

Научись сам решать задачи изучив физику на этой странице:
Услуги:

Готовые задачи по физике которые сегодня купили:

  1. Ион с зарядом q  Ze ( e – элементарный заряд) и массой m A mp   ( mp – масса протона) ускоряется разностью потенциалов U и влетает в однородное магнитное поле напряженностью H перпендикулярно его силовым линиям.
  2. Два одинаковых заряженных шарика отталкиваются друг от друга.
  3. Две батареи с электродвижущими силами 1  и 2  и внутренними сопротивлениями 1 r и 2 r соединены разноименными полюсами и подключены к внешнему сопротивлению R .
  4. Определить суммарный импульс электронов в прямом проводе длиной 700 м, по которому течет ток 15 А.
  5. Металлический шар радиусом R заряжен равномерно с поверхностной плотностью .
  6. Колебательный контур имеет емкость C  4 мкФ , индуктивность L  2 мГн и активное сопротивление R  10 Ом .
  7. Уравнение вращения диска радиусом R  1 м имеет вид 3   3 t  0,1t .
  8. Тонкий обруч радиусом 2 м, подвешенный на вбитый в стену гвоздь, колеблется в плоскости, параллельной стене.
  9. Тонкий очень длинный стержень равномерно заряжен с линейной плотностью 50 мкКл/м.
  10. Определить скорость распространения волны в неупругой среде, если разность фаз колебаний двух точек среды, отстоящих друг от друга на расстоянии x  10 см , равна 3   .