| 🎓 Заказ №: 21964 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Физика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 149 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
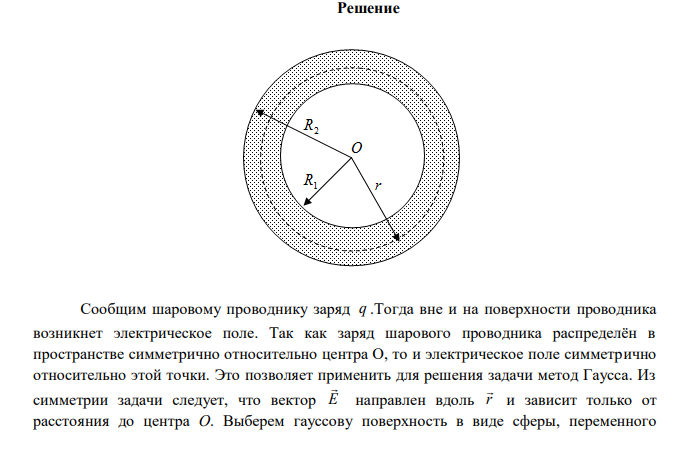
Определить емкость С уединенного шарового проводника радиуса R1 0,20 м окруженного прилегающим к нему концентрическим слоем однородного изотропного диэлектрика с наружным радиусом R2 0,40 м . Диэлектрическая проницаемость 2.
Решение Сообщим шаровому проводнику заряд q .Тогда вне и на поверхности проводника возникнет электрическое поле. Так как заряд шарового проводника распределён в пространстве симметрично относительно центра О, то и электрическое поле симметрично относительно этой точки. Это позволяет применить для решения задачи метод Гаусса. Из симметрии задачи следует, что вектор E направлен вдоль r и зависит только от расстояния до центра О. Выберем гауссову поверхность в виде сферы, переменного радиуса r с центром в точке О. Учтем, что модуль напряжённости поля одинаков во всех точках этой поверхности и En E . Для определения напряженности E проведем гауссову поверхность S (штрихпунктирная область) радиусом r и воспользуемся теоремой Остроградского–Гаусса: E dS q S n 0 1 Поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме всех зарядов, расположенных внутри поверхности, деленной на ε0 Где 0 =8,85·10−12 Ф/м – электрическая постоянная; – диэлектрическая проницаемость среды.. Из соображения симметрии E E const n , тогда Е можно вынести за знак интеграла: 0 q ES Площадь сферы равна 2 S 4r Тогда из двух последних выражений имеем: 0 2 4 q E r Отсюда: 2 4 0 r q E


| Научись сам решать задачи изучив физику на этой странице: |
| Услуги: |
Готовые задачи по физике которые сегодня купили:
- Две пружины жесткостью м кН k1 0,5 и м кН k2 1 скреплены параллельно. Определить потенциальную энергию П данной системы при абсолютной деформации l 4 см .
- Какой изотоп образуется из 92U 239 после двух β и одного α-распада?
- В результате рассеяния фотона с длиной волны 2 пм на свободном электроне комптоновское смещение оказалось равным 1,2 пм.
- Нить с привязанными к ее концам грузами массами m 50 г 1 и m 60 г 2 перекинута через блок диаметром D=4 см.
- Ток в цепи батареи, ЭДС которой 30 В, равен I 3 A.
- Катушка диаметром D 10см , состоящая из N 500 витков, находится в магнитном поле.
- Определить частоту v простых гармонических колебаний диска радиусом R=20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.
- Два бесконечно длинных проводника и круговой виток расположены так, как это показано на рисунке.
- На ступенчатый вал (рис. 3), радиусы которого R 0,2 м и r 0,1м намотаны в противоположных направлениях нити, нагруженные одинаковыми массами m 0,1 кг.
- Вычислить энергию ядерной реакции H H He n 1 0 4 2 3 1 2 1 .
