Для связи в whatsapp +905441085890

На рис. 16.1.  1 1,0 B ,  2  2,0 B ,  3  3,0 B , r1 1,0 Ом , r2  0,5 Ом , r Ом 3 1 3  , R1 1,0 Ом , R Ом 3 1 3  .

🎓 Заказ №: 21960
⟾ Тип работы: Задача
📕 Предмет: Физика
✅ Статус: Выполнен (Проверен преподавателем)
🔥 Цена: 149 руб.

👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.

➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.

➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.

⚡ Условие + 37% решения:

На рис. 16.1.  1 1,0 B ,  2  2,0 B ,  3  3,0 B , r1 1,0 Ом , r2  0,5 Ом , r Ом 3 1 3  , R1 1,0 Ом , R Ом 3 1 3  . Определите: 1) силы тока во всех участках цепи; 2) тепловую мощность, которая выделяется на сопротивлении R3 .

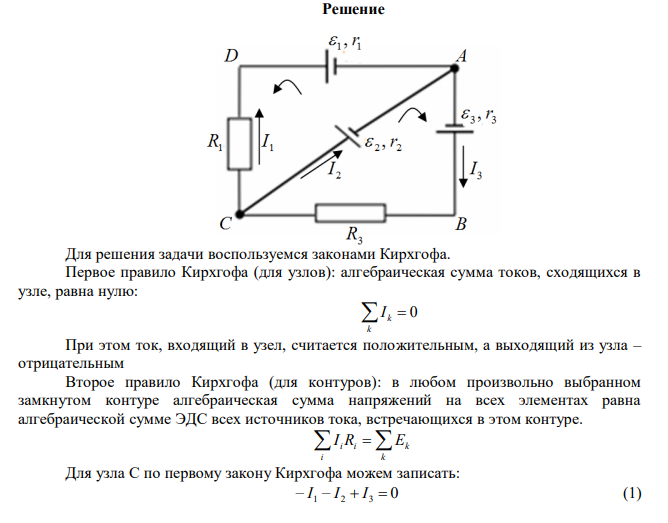
Решение Для решения задачи воспользуемся законами Кирхгофа. Первое правило Кирхгофа (для узлов): алгебраическая сумма токов, сходящихся в узле, равна нулю:   k k I 0 При этом ток, входящий в узел, считается положительным, а выходящий из узла – отрицательным Второе правило Кирхгофа (для контуров): в любом произвольно выбранном замкнутом контуре алгебраическая сумма напряжений на всех элементах равна алгебраической сумме ЭДС всех источников тока, встречающихся в этом контуре.    i k iRi Ek I Для узла C по первому закону Кирхгофа можем записать:  I 1  I 2  I 3  0 (1) Обход контура ABCA выберем за часовой стрелкой. Тогда для этого контура по второму закону Кирхгофа можем записать уравнение:   2 2 3 3 3 3 2 I r  I R  r    (2) Обход контура ADCA выберем против часовой стрелки. Тогда для этого контура по второму закону Кирхгофа можем записать   1 1 1 2 2 1 2  I R  r  I r    (3) Подставим данные в (2): 1 3 2 0,5I 2  I3  (4) Подставим данные в (3):  2I 1  0,5I 2  1 (5)

На рис. 16.1.  1 1,0 B ,  2  2,0 B ,  3  3,0 B , r1 1,0 Ом , r2  0,5 Ом , r Ом 3 1 3  , R1 1,0 Ом , R Ом 3 1 3  . Определите: 1) силы тока во всех участках цепи; 2) тепловую мощность, которая выделяется на сопротивлении R3 .
На рис. 16.1.  1 1,0 B ,  2  2,0 B ,  3  3,0 B , r1 1,0 Ом , r2  0,5 Ом , r Ом 3 1 3  , R1 1,0 Ом , R Ом 3 1 3  . Определите: 1) силы тока во всех участках цепи; 2) тепловую мощность, которая выделяется на сопротивлении R3 .
На рис. 16.1.  1 1,0 B ,  2  2,0 B ,  3  3,0 B , r1 1,0 Ом , r2  0,5 Ом , r Ом 3 1 3  , R1 1,0 Ом , R Ом 3 1 3  . Определите: 1) силы тока во всех участках цепи; 2) тепловую мощность, которая выделяется на сопротивлении R3 .

Научись сам решать задачи изучив физику на этой странице:
Услуги:

Готовые задачи по физике которые сегодня купили:

  1. На шелковой нити подвешен маленький шарик массой m=0,1 г, несущий на себе заряд Q.
  2. Колесо вращается вокруг неподвижной оси так, что угол поворота зависит от времени по закону 3   2  6t  2t .
  3. Тепловая машина работает в интервале температур 500 0С и 20 0С.
  4. Плоско поляризованный свет падает на призму Николя и полностью гасится.
  5. Определите (с точностью до целого числа), чему равно соотношение коэффициентов диффузии водорода и кислорода 2 2 O H D D , находящихся при одинаковых условиях.
  6. Уравнение колебаний материальной точки массой 16 г имеет вид x t см, с 4 0,2sin 0,25.
  7. В опыте Юнга источник испускает свет с длинами волн 1  0,45 мкм и 2  0,54 мкм .
  8. При фотоэффекте с платиновой поверхности величина задерживающего потенциала оказалась равной 0,8 В.
  9. Расстояние между пластинами плоского конденсатора с диэлектриком слюды равно 2 мм, а напряжение между пластинами 200 В.
  10. Какой угол с вертикалью составит нить, на которой висит шарик массой 25 мг, если поместить шарик в горизонтальное однородное электрическое поле с напряженностью м В E  35 , сообщив ему заряд q  7 мкКл?