| 🎓 Заказ №: 21917 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Физика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 149 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
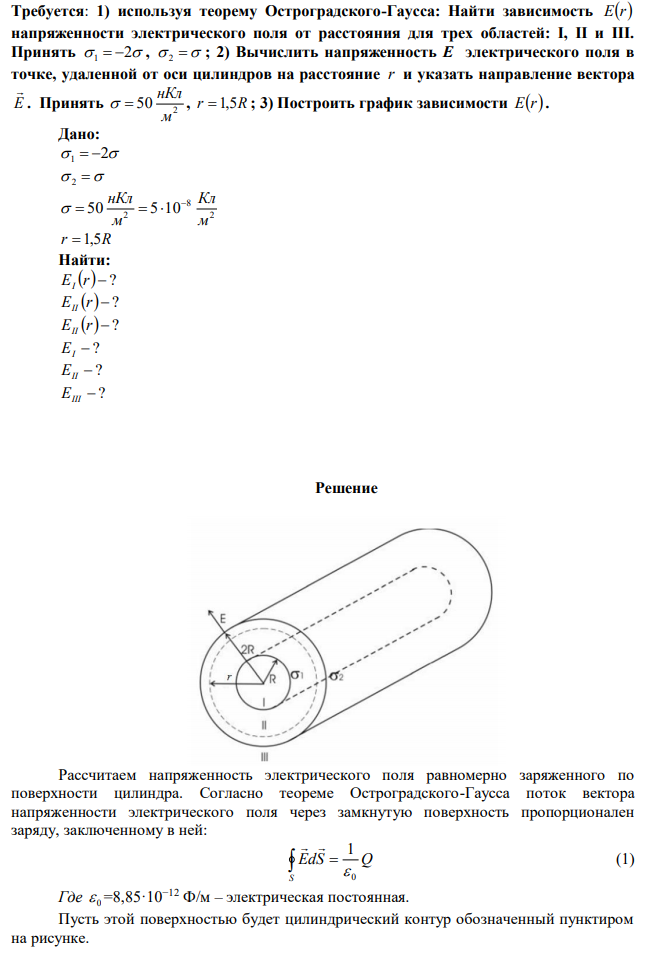
На двух коаксиальных бесконечных цилиндрах радиусами R и 2R равномерно распределены заряды с поверхностными плотностями 1 и 2 (рис. 3.3). Требуется: 1) используя теорему Остроградского-Гаусса: Найти зависимость Er напряженности электрического поля от расстояния для трех областей: I, II и III. Принять 1 2 , 2 ; 2) Вычислить напряженность E электрического поля в точке, удаленной от оси цилиндров на расстояние r и указать направление вектора E . Принять 2 50 м нКл , r 1,5R ; 3) Построить график зависимости Er.
Решение Рассчитаем напряженность электрического поля равномерно заряженного по поверхности цилиндра. Согласно теореме Остроградского-Гаусса поток вектора напряженности электрического поля через замкнутую поверхность пропорционален заряду, заключенному в ней: EdS Q S 0 1 (1) Где 0 =8,85·10−12 Ф/м – электрическая постоянная. Пусть этой поверхностью будет цилиндрический контур обозначенный пунктиром на рисунке. Для расчета интеграла по поверхности необходимо выбрать удобную поверхность интегрирования. В данном случае, исходя из симметрии задачи, таковой будет являться поверхность в виде цилиндра радиуса r высотой H , коаксиального данным цилиндрам. Из симметрии задачи также следует, что вектор напряженности электрического поля E будет сонаправлен с вектором dS перпендикулярным к боковой поверхности выбранного цилиндра, и модуль будет постоянным во всех точках этой поверхности (это справедливо для длинного цилиндра). На основаниях цилиндра вектор E будет перпендикулярен вектору нормали к основаниям, и скалярное произведение EdS будет равно нулю. Тогда интеграл выражения (1) будет равен: EdS E r H Q S 0 1 2 (2) Отсюда: r H Q E 2 0 (3) Учтем, что поверхностная плотность заряда равна: RH Q S Q 2 (4) Где R – радиус цилиндра. Отсюда: Q 2RH (5) Подставим (5) в (3): r R r H RH E 2 0 0 2 (6)


| Научись сам решать задачи изучив физику на этой странице: |
| Услуги: |
Готовые задачи по физике которые сегодня купили:
- В вершинах квадрата находятся одинаковые заряды Q1 = Q2 = Q3 = Q4 = 8·10-10 Кл.
- Четверть тонкого кольца радиусом R = 10 см несет равномерно распределенный заряд Q = 0,05 мкКл.
- Уравнение звуковой волны в воде дано в виде: y t x 5 4 3,2 10 cos1630 6,6 10 (мм).
- Два заряда q1 3q и q2 q (где 9 10 q Кл) находятся на расстоянии 12 см друг от друга.
- Найти силу тяги, развиваемую мотором автомобиля, движущегося в гору с ускорением 2 1 с м a .
- Два металлических шарика радиусами R1 = 5 см и R2 = 10 см имеют заряды Q1=40 нКл и Q2 = -20 нКл соответственно.
- Две параллельные заряженные плоскости, поверхностные плотности которых 1 2 2 м мкКл и 2 2 0,8 м мкКл , находятся на расстоянии d 0,6 см друг от друга.
- Два конденсатора емкостями C1 5 мкФ и C2 8 мкФ соединены последовательно и присоединены к батареи с ЭДС 80 В .
- Поле образовано точечным диполем с электрическим моментом р = 200 пКл·м.
- По двум бесконечно длинным прямым проводам, скрещенным под прямым углом, текут токи I 1 30 А и I 2 40 А .
