Магнитный момент pm тонкого проводящего кольца 2 pm  5 А м.

🎓 Заказ №: 21914

⟾ Тип работы: Задача

📕 Предмет: Физика

✅ Статус: Выполнен (Проверен преподавателем)

🔥 Цена: 149 руб.

👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.

➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.

➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.

⚡ Условие + 37% решения:

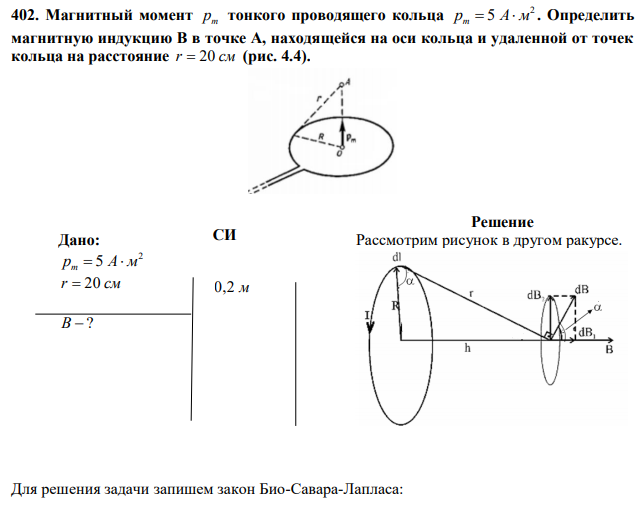
Магнитный момент pm тонкого проводящего кольца 2 pm  5 А м . Определить магнитную индукцию В в точке А, находящейся на оси кольца и удаленной от точек кольца на расстояние r  20 см (рис. 4.4).

Решение Рассмотрим рисунок в другом ракурсе. Для решения задачи запишем закон Био-Савара-Лапласа: Решение Количество теплоты выделяющееся в проводнике при прохождении тока за время dt на основании закона Джоуля – Ленца равно: dQ I Rdt 2  (1) Тогда полная теплота равна:     t t t t e I R Q I Rdt I e Rdt    2 2 0 0 2 0 0 2 1 2         СИ Решение СИ Рассмотрим рисунок в другом ракурсе. 0,2 м   3 0 , 4 r I dl r dB       (1) Где dB  – магнитная индукция поля, создаваемая элементом тока Idl в точке, определяемой радиус-вектором r  ; r – модуль радиус-вектора; м 7 Гн 0 4 10     – магнитная постоянная. Выделим на кольце элемент dl и от него в точку проведем радиус-вектор r. Вектор dB  направим в соответствии с правилом буравчика. Согласно принципу суперпозиции магнитных полей, магнитная индукция B в точке определяется интегрированием:   l B dB   Где символ l означает, что интегрирование распространяется на всю длину кольца. Разложим вектор dB  на две составляющие: dB dB1 dB2      Тогда     l l B dB1 dB2    Учтем из соображений симметрии, что 2  0

Научись сам решать задачи изучив физику на этой странице: Решение задач по физике

Услуги: Заказать физику Помощь по физике

Готовые задачи по физике которые сегодня купили:

1. При распаде 4 2 235 92 239 94Pu  U  He освобождается энергия, большая часть которой составляет кинетическую энергию  частиц.
2. Найти напряженность магнитного поля между полюсами электромагнита, если проводник массой 10 г и длиной 1м при токе в нем 19,6 А висит в поле, не падая.
3. Закон изменения разности потенциалов на обкладках конденсатора в контуре задан уравнением U t 4  50cos10 (В).
4. Электрон, обладавший кинетической энергией Т = 10 эВ, влетел в однородное электрическое поле в направлении силовых линий поля.
5. В азоте взвешены мельчайшие пылинки, которые движутся так, как если бы они были очень крупными молекулами.
6. К грузу массой 7 кг подвешен на верёвке груз массой 5 кг.
7. Сила тока в проводнике с сопротивлением R  10 Ом изменяется со временем по закону t I I e   0 , где I 0  20 А , 2 1 10    c.
8. Движение двух материальных точек описывается уравнениями.
9. На картонный каркас длиной l = 0,8 м и диаметром D = 4 см намотан в один слой провод диаметром d = 0,25 мм так, что витки плотно прилегают друг к другу.
10. В однородном магнитном поле с индукцией B  0,5 Тл вращается с частотой 1 10  n  c стержень длиной l  20 см.