| 🎓 Заказ №: 21941 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Физика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 149 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
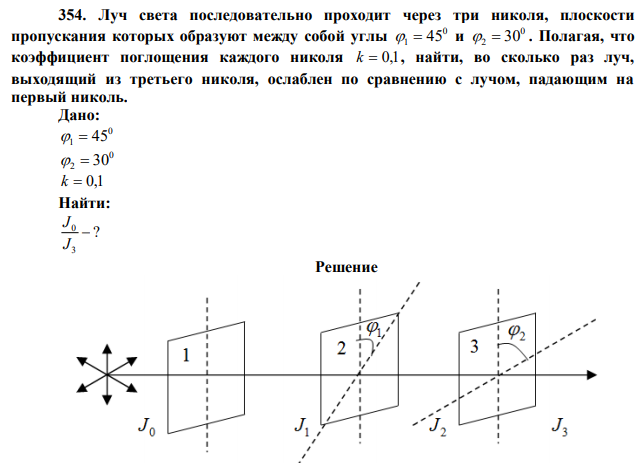
Луч света последовательно проходит через три николя, плоскости пропускания которых образуют между собой углы 0 1 45 и 0 2 30 . Полагая, что коэффициент поглощения каждого николя k 0,1 , найти, во сколько раз луч, выходящий из третьего николя, ослаблен по сравнению с лучом, падающим на первый николь.
Решение Естественный свет, попадая на поляризатор 1 (первый николь) П , расщепляется вследствие двойного лучепреломления на два луча: обыкновенный (о) и необыкновенный (е). Оба луча одинаковы по интенсивности и полностью поляризованы. Плоскость колебаний необыкновенного луча лежит в плоскости чертежа (плоскость главного сечения). Плоскость колебаний обыкновенного луча перпендикулярна плоскости чертежа. Обыкновенный луч о вследствие полного внутреннего отражения от границы СВ отбрасывается на зачерненную поверхность призмы и поглощается ею. Необыкновенный луч е проходит через призму, уменьшая свою интенсивность вследствие поглощения. Таким образом, интенсивность света, прошедшего через поляризатор (первый николь) равна: 1 0 1 1 2 1 J J k (1) где 0 J – интенсивность естественного света; 1 k – коэффициент потерь в первом николе. Плоско поляризованный луч света интенсивностью J1 падает на анализатор А (второй николь) и также расщепляется на два луча различной интенсивности: обыкновенный и необыкновенный. Согласно закону Малюса, интенсивность необыкновенного луча, вышедшего из второго николя с коэффициента потерь: 1 2 2 1 2 J J 1 k cos (2)

| Научись сам решать задачи изучив физику на этой странице: |
| Услуги: |
Готовые задачи по физике которые сегодня купили:
- Найти температуру газообразного азота, при которой абсолютным скоростям молекул c м 1 300 и c м 2 600 соответствуют одинаковые значения функции распределения Максвелла.
- Колебательный контур с конденсатором емкостью 100 пФ настроен на длину волны 30 м
- Индукция магнитного поля между полюсами двухполюсного генератора равна 0,8 Тл.
- Два одинаковых шарика с массами m 1 г каждый подвешены в одной точке на тонких непроводящих нитях одинаковой длины l 2 м.
- Найти число электронов в атоме, у которого в основном состоянии заполнены K, L, M-слои и 4s, 4p-оболочки полностью, а 4d-оболочка – наполовину.
- Два шарика массой 1 г каждый подвешены на нитях, верхние концы которых соединены вместе.
- Период затухающих колебаний 4 с, логарифмический декремент затухания 1,6, начальная фаза φ0 = 0, при t = T/4 смещение точки 4,5 см.
- Точка одновременно совершает два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями x=A1sin и y=A2cost где A1 = 3 см, A2 = 2 см
- Прямоугольная катушка гальванометра размерами 3×2 см имеет 400 витков тонкой проволоки
- Определить период затухающих колебаний, если период собственных колебаний 2 с, а логарифмический декремент затухания 0,314
