Интегрирование четных и нечетных функций в симметричных пределах
Пусть функция  непрерывна на отрезке
непрерывна на отрезке 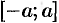 , симметричном относительно точки
, симметричном относительно точки 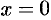 . Докажем, что
. Докажем, что
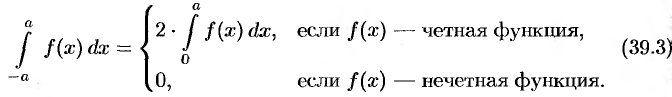
Разобьем отрезок интегрирования 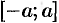 на части
на части 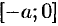 и
и 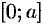 . Тогда по свойству аддитивности
. Тогда по свойству аддитивности
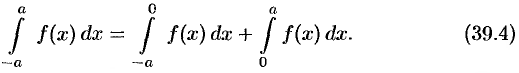
В первом интеграле сделаем подстановку 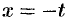 . Тогда
. Тогда
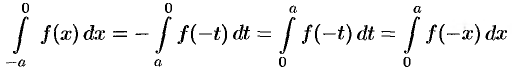
(согласно свойству: «определенный интеграл не зависит от обозначения переменной интегрирования»). Возвращаясь к равенству (39.4), получим
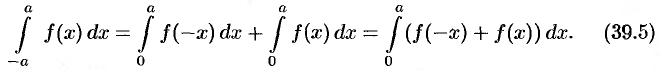
Если функция  четная
четная 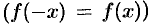 , то
, то 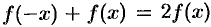 ; если функция
; если функция  нечетная
нечетная 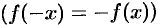 , то
, то 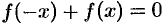 .
.
Следовательно, равенство (39.5) принимает вид (39.3).
Благодаря доказанной формуле можно, например, сразу, не производя вычислений, сказать, что
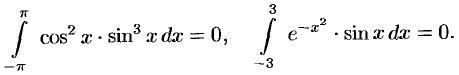
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Конус второго порядка |
| Работа переменной силы в определённом интеграле |
| Давление жидкости на вертикальную пластинку |
| Вычисление статических моментов и координат центра тяжести плоской кривой |

