| 🎓 Заказ №: 22506 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Экономика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 249 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
Известна функция полезности типичного потребителя 𝑈 = √𝑞𝑥 + √𝑞𝑦, цены 𝑃𝑥 = 1, 𝑃𝑦 = 2 ден. ед., доход потребителя 𝑚 = 60 ден. ед. 1). Найти оптимальный объем потребления товаров 𝑥 и 𝑦. 2). Администрация города решила повысить уровень благосостояния граждан, субсидируя потребление товара 𝑦 в размере, равном половине его рыночной цены. На сколько возрастет потребление товаров 𝑥 и 𝑦? В какую сумму обойдется эта программа городской администрации (в расчете на одного потребителя)?
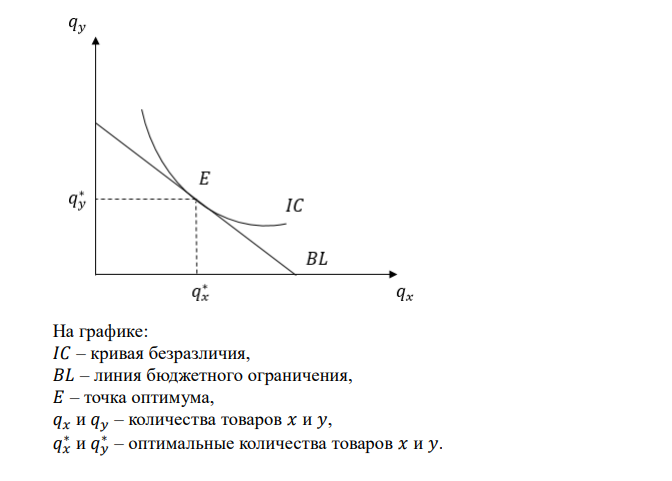
Решение 1). Оптимальный набор товаров 𝑥 и 𝑦 , максимизирующий получаемую потребителем полезность, графически представляет собой точку касания линией бюджетного ограничения потребителя одной из его кривых безразличия: На графике: 𝐼𝐶 – кривая безразличия, 𝐵𝐿 – линия бюджетного ограничения, 𝐸 – точка оптимума, 𝑞𝑥 и 𝑞𝑦 – количества товаров 𝑥 и 𝑦, 𝑞𝑥 ∗ и 𝑞𝑦 ∗ – оптимальные количества товаров 𝑥 и 𝑦. В точке потребительского оптимума угол наклона касательной к кривой безразличия 𝑀𝑅𝑆𝑥𝑦 = 𝑀𝑈𝑥⁄𝑀𝑈𝑦 равен углу наклона линии бюджетного ограничения 𝑃𝑥⁄𝑃𝑦. Тогда оптимальный объем потребления товаров 𝑥 и 𝑦 можно определить из решения следующей системы уравнений: { 𝑀𝑈𝑥⁄𝑀𝑈𝑦 = 𝑃𝑥⁄𝑃𝑦 𝑞𝑥𝑃𝑥 + 𝑞𝑦𝑃𝑦 = 𝑚 . Здесь 𝑀𝑈𝑥⁄𝑀𝑈𝑦 = 𝑃𝑥⁄𝑃𝑦 – правило максимизации полезности потребителя (внутреннее решение задачи потребительского выбора), 𝑞𝑥𝑃𝑥 + 𝑞𝑦𝑃𝑦 = 𝑚 – его бюджетное ограничение. Находим функции предельных полезностей как условную производную функции совокупной полезности по соответствующей переменной: 𝑀𝑈𝑥 = 𝜕𝑈⁄𝜕𝑞𝑥 = (√𝑞𝑥 + √𝑞𝑦) ` = 0,5𝑞𝑥 −0,5 ; 𝑀𝑈𝑦 = 𝜕𝑈⁄𝜕𝑞𝑦 = (√𝑞𝑥 + √𝑞𝑦) ` = 0,5𝑞𝑦 −0,5 . Подставляем известные значения в систему уравнений и находим параметры потребительского оптимума: { 0,5𝑞𝑥 −0,5 0,5𝑞𝑦 −0,5 ⁄ = 1⁄2 1𝑞𝑥 + 2𝑞𝑦 = 60 ; { √𝑞𝑦⁄√𝑞𝑥 = 0,5 𝑞𝑥 = 60 − 2𝑞𝑦 ; { √𝑞𝑦 = 0,5√𝑞𝑥 𝑞𝑥 = 60 − 2𝑞𝑦 . Подставляем выражение для 𝑞𝑥 в верхнее равенство: √𝑞𝑦 = 0,5√60 − 2𝑞𝑦; 𝑞𝑦 = 0,25 · (60 − 2𝑞𝑦); 1,5𝑞𝑦 = 15; 𝑞𝑦 ∗ = 10.


| Научись сам решать задачи изучив экономику на этой странице: |
| Услуги: |
Готовые задачи по экономике которые сегодня купили:
- Фирма выпускает продукцию и продает ее на конкурентном рынке по цене 40.
- Среднемесячный уровень инфляции в России в первом квартале 2015 года составил 2,42%.
- Определить прибыль от реализации продукции, если предприятие выпустило изделий А – 1000 шт., изделий В – 2500 шт.
- Определить на основе понятия внутренней нормы доходности, выгоден ли описанный в предыдущем примере вариант покупки сельскохозяйственного предприятия для инвестора, если он ожидает доходность на уровне 12% годовых; 20%?
- Функция общих издержек совершенного конкурента выглядит так: TC = 100 + 4Q + 0,25Q2 .
- При условии, что государственные закупки составили 650 млрд ден. ед., налоговые поступления – 850 млрд ден. ед., трансферты – 300 млрд ден. ед., обслуживание государственного долга — 120 млрд ден. ед., государственный бюджет исполнен с:
- Найти изменение текущей рыночной стоимости облигации со сроком обращения 10 лет, номинальной стоимостью 25000 руб., купонной ставкой 202 10% и доходностью к погашению 8% при увеличении и уменьшении доходности к погашению на 2%.
- Банк предлагает 17% годовых за размещение денежных средств на открываемых им депозитных счетах.
- В банке берется кредит 250 тысяч рублей сроком на 3 года под сложную процентную ставку 14%.
- Чистый вес изделия, изготовленного из стали – 99 кг, норма расхода стали – 111 кг.
